Toán 7, giải toán lớp 7 cánh diều Bài tập cuối chương VII trang 119 SGK Toán 7 cánh diều

Giải bài 6 trang 119 SGK Toán 7 tập 2 - Cánh diều


Cho tam giác ABC cân tại A có

Đề bài

Cho tam giác ABC cân tại A có \(\widehat {ABC} = 70^\circ \). Hai đường cao BD và CE cắt nhau tại H.

a) Tính số đo các góc còn lại của tam giác ABC.

b) Chứng minh BD = CE.

c) Chứng minh tia AH là tia phân giác của góc BAC.

Phương pháp giải - Xem chi tiết

a) Tam giác ABC cân tại A nên số đo góc B bằng số đo góc C và tổng ba góc trong một tam giác bằng 180°.

b) Chứng minh hai tam giác vuông ADB và AEC bằng nhau.

c) Chứng minh \(\widehat {BAH} = \widehat {CAH}\).

Lời giải chi tiết

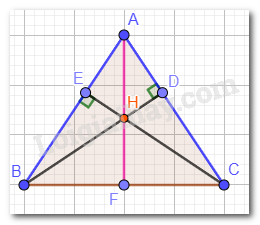
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).

Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ  - 70^\circ  - 70^\circ  = 40^\circ \).

b) Xét tam giác vuông ADB và tam giác vuông AEC có:

     AB = AC (tam giác ABC cân);

     \(\widehat A\) chung.

Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).

c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.

Xét hai tam giác vuông AFB và AFC có:

     AB = AC (tam giác ABC cân);

     AF chung.

Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).

Vậy tia AH là tia phân giác của góc BAC.


Bình chọn:
3.8 trên 8 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 7 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store