Giải bài 6 trang 113 vở thực hành Toán 9 tập 2

Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Chứng minh rằng (AH = 2OM).

Đề bài

Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Chứng minh rằng $AH = 2OM$.

Phương pháp giải - Xem chi tiết

+ Kẻ đường cao CD của tam giác ABC. Gọi N là trung điểm của cạnh AC.

+ Chứng minh $\widehat {AON} = \frac{{\widehat {AOC}}}{2} = \widehat {ABC}$, suy ra $\widehat {NAO} = {90^o} - \widehat {AON} = {90^o} - \widehat {ABC} = \widehat {DAH}$.

+ Chứng minh tương tự ta có: $\widehat {MCO} = {90^o} - \widehat {MOC} = \widehat {DCA}$

+ Chứng minh $\Delta NAO\backsim \Delta DAH\left( g.g \right)$, suy ra $AH = \frac{{AO.DA}}{{AN}} = \frac{{2AO.DA}}{{AC}}.$

+ Chứng minh $\Delta OMC\backsim \Delta ADC\left( g.g \right)$ nên $2OM = \frac{{2OC.AD}}{{AC}} = \frac{{2OA.DA}}{{AC}} = AH$

Lời giải chi tiết

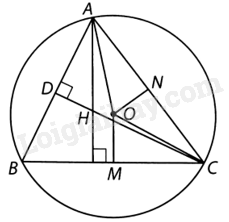
Kẻ đường cao CD của tam giác ABC. Gọi N là trung điểm của cạnh AC. Khi đó tam giác AOC cân tại O nên ON cũng là phân giác của góc AOC. Vậy $\widehat {AON} = \frac{{\widehat {AOC}}}{2} = \widehat {ABC}$.

Suy ra $\widehat {NAO} = {90^o} - \widehat {AON} = {90^o} - \widehat {ABC} = \widehat {DAH}$.

Tương tự $\widehat {MCO} = {90^o} - \widehat {MOC} = \widehat {DCA}$.

Hai tam giác NAO và DAH có: $\widehat {NAO} = \widehat {DAH}$ (chứng minh trên), $\widehat {ANO} = \widehat {ADH} = {90^o}$. Do đó, $\Delta NAO\backsim \Delta DAH\left( g.g \right)$. Suy ra $\frac{{AO}}{{AH}} = \frac{{AN}}{{DA}}$, hay $AH = \frac{{AO.DA}}{{AN}} = \frac{{2AO.DA}}{{AC}}.\left( 1 \right)$

Hai tam giác OMC và ADC có: $\widehat {MCO} = \widehat {DCA}$ (chứng minh trên), $\widehat {OMC} = \widehat {ADC} = {90^o}$.

Do đó, $\Delta OMC\backsim \Delta ADC\left( g.g \right)$. Suy ra $\frac{{OM}}{{AD}} = \frac{{OC}}{{AC}}$. Do đó

$2OM = \frac{{2OC.AD}}{{AC}} = \frac{{2OA.DA}}{{AC}} = AH$ (theo (1)).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 113 vở thực hành Toán 9 tập 2
Cho một lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng lục giác đều có diện tích (6sqrt 3 c{m^2}), hãy tính độ dài cạnh của hình vuông đã cho.
Giải bài 5 trang 112 vở thực hành Toán 9 tập 2
Bạn Lan muốn cắt hình ngôi sao có dạng như hình dưới đây (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu độ?
Giải bài 4 trang 112 vở thực hành Toán 9 tập 2
a) Cho hình vuông ABCD nội tiếp đường tròn (O) như hình bên. Phép quay thuận chiều ({45^o}) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ như hình bên. Hãy vẽ tứ giác A’B’C’D’. b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
Giải bài 3 trang 111 vở thực hành Toán 9 tập 2
Cho một hình lục giác đều và một hình vuông cùng nội tiếp một đường tròn. Biết rằng hình vuông có cạnh bằng 3cm. Tính chu vi và diện tích của hình lục giác đều đã cho.
Giải bài 2 trang 111 vở thực hành Toán 9 tập 2
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Giải bài 1 trang 110, 111 vở thực hành Toán 9 tập 2
Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng: a) Tứ giác AEHF nội tiếp đường tròn tâm I; b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF.
Giải câu hỏi trắc nghiệm trang 110 vở thực hành Toán 9 tập 2
Khẳng định nào sau đây là đúng? A. Góc nội tiếp có số đo bằng số đo cung bị chắn. B. Góc có hai cạnh chứa các dây cung của đường tròn là góc nội tiếp đường tròn đó. C. Góc nội tiếp có số đo bằng một nửa số đo cung bị chắn. D. Góc có đỉnh nằm trên đường tròn là góc nội tiếp đường tròn đó.