 Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
 Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn ..
Bài 15. Độ dài của cung tròn. Diện tích hình quạt tròn ..
Giải bài 5 trang 107 vở thực hành Toán 9
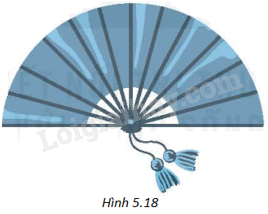
Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 2,2dm như Hình 5.18. Tính diện tích phần giấy của chiếc quạt khi gấp lại, phần giấy có chiều dài khoảng 1,6dm (làm tròn kết quả đến hàng phần trăm của (d{m^2})).
Đề bài
Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 2,2dm như Hình 5.18. Tính diện tích phần giấy của chiếc quạt khi gấp lại, phần giấy có chiều dài khoảng 1,6dm (làm tròn kết quả đến hàng phần trăm của \(d{m^2}\)).
Phương pháp giải - Xem chi tiết
Diện tích \({S_v}\) của hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính R và r là: \({S_v} = \pi \left( {{R^2} - {r^2}} \right)\) (với \(R > r\)).
Lời giải chi tiết
Diện tích phần giấy cần tính bằng nửa diện tích hình vành khuyên tạo bởi hai đường tròn có bán kính là 2,2dm và 0,6dm. Diện tích phần giấy của chiếc quạt đó là: \(S = \frac{1}{2}\pi \left( {{{2,2}^2} - {{0,6}^2}} \right) \approx 7,04\left( {d{m^2}} \right)\).
- Giải bài 6 trang 107 vở thực hành Toán 9
- Giải bài 4 trang 106 vở thực hành Toán 9
- Giải bài 3 trang 106 vở thực hành Toán 9
- Giải bài 2 trang 106 vở thực hành Toán 9
- Giải bài 1 trang 105, 106 vở thực hành Toán 9
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay











