 Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT
 Bài 14. Cung và dây của một đường tròn trang 100, 101, ..
Bài 14. Cung và dây của một đường tròn trang 100, 101, ..
Giải bài 5 trang 103, 104 vở thực hành Toán 9
Cho đường tròn (O; R). Gọi H là điểm thuộc bán kính OA sao cho (OH = frac{{sqrt 3 }}{2}OA). Dây CD vuông góc với OA tại H. Tính số đo cung lớn CD.
Đề bài
Cho đường tròn (O; R). Gọi H là điểm thuộc bán kính OA sao cho \(OH = \frac{{\sqrt 3 }}{2}OA\). Dây CD vuông góc với OA tại H. Tính số đo cung lớn CD.
Phương pháp giải - Xem chi tiết
+ Tam giác OHC vuông tại H có: \(\cos \widehat {HOC} = \frac{{OH}}{{OC}} = \frac{{\frac{{\sqrt 3 }}{2}OA}}{{OA}} = \frac{{\sqrt 3 }}{2}\) nên tính được góc HOC.
+ Chứng minh OH là đường cao đồng thời là đường phân giác, từ đó tính được góc COD.
+ Số đo cung nhỏ CD bằng số đo góc COD, số đo cung lớn CD bằng 360 độ trừ đi số đo cung nhỏ CD.
Lời giải chi tiết
(H.5.13)
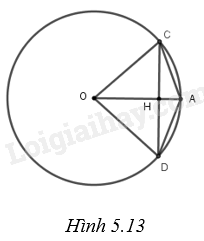
Xét đường tròn (O) có OH vuông góc với CD tại H nên H là trung điểm của CD. Xét tam giác OHC vuông tại H có:
\(\cos \widehat {HOC} = \frac{{OH}}{{OC}} = \frac{{\frac{{\sqrt 3 }}{2}OA}}{{OA}} = \frac{{\sqrt 3 }}{2}\). Suy ra \(\widehat {HOC} = {30^o}\).
Mà tam giác OCD cân tại O \(\left( {OC = OD = R} \right)\) có OH là đường cao đồng thời là đường phân giác, suy ra \(\widehat {COD} = 2\widehat {COH} = {60^o}\)
Do đó, số đo cung nhỏ CD bằng \({60^o}\) và số đo cung lớn CD bằng \({360^o} - {60^o} = {300^o}\).
- Giải bài 4 trang 103 vở thực hành Toán 9
- Giải bài 3 trang 102, 103 vở thực hành Toán 9
- Giải bài 2 trang 102 vở thực hành Toán 9
- Giải bài 1 trang 102 vở thực hành Toán 9
- Giải câu hỏi trắc nghiệm trang 101 vở thực hành Toán 9
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Kết nối tri thức - Xem ngay











