Giải bài 3.21 trang 39 sách bài tập toán 8 - Kết nối tri thức với cuộc sống

Hai đường trung tuyến BM, CN của tam giác ABC cân tại A cắt nhau tại G. Gọi H, K lần lượt là điểm sao cho trung điểm của GH là M, trung điểm của GK là N.

Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Đề bài

Hai đường trung tuyến BM, CN của tam giác ABC cân tại A cắt nhau tại G. Gọi H, K lần lượt là điểm sao cho trung điểm của GH là M, trung điểm của GK là N. Chứng minh tứ giác BCHK là hình chữ nhật.

Phương pháp giải - Xem chi tiết

Sử dụng kiến thức về dấu hiệu nhận biết hình chữ nhật để chứng minh: Hình bình hành có một góc vuông là hình chữ nhật.

Lời giải chi tiết

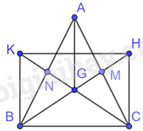
Vì BM, CN là hai đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC, AB. Hai đường trung tuyến này cắt nhau tại G nên G là trọng tâm của tam giác ABC. Do đó, AG là đường trung tuyến của tam giác.

Mà tam giác ABC cân tại A nên AG là đường trung tuyến đồng thời là đường cao. Suy ra \(AG \bot BC\)

Do M là trung điểm của AC và GH nên tứ giác AGCH là hình bình hành, do đó \(HC = AG\), HC//AG

Do N là trung điểm của AB và KG nên tứ giác AKBG là hình bình hành, do đó \(KB = AG,\) KB//AG

Do đó, \(HC = KB,HC//KB\)

Suy ra, tứ giác KBCH là hình bình hành.

Vì \(AG \bot BC\) nên \(KB \bot BC\) nên \(\widehat {KBC} = {90^0}\)

Vậy tứ giác BCHK là hình chữ nhật.

Bình luận

Chia sẻ

Bình chọn:

4 trên 9 phiếu

Bài tiếp theo

Giải bài 3.22 trang 39 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
1. Sử dụng tính chất tổng các góc của một tam giác bằng \({180^0}\) để chứng minh:
Giải bài 3.20 trang 39 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
Cho tam giác ABC cân tại A, AH là đường cao. Gọi M, N lần lượt là trung điểm của AB, AC. Gọi D, E lần lượt là điểm sao cho M là trung điểm của HD, N là trung điểm của HE.

Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý