-
Toán 8 tập 1 - Kết nối tri thức với cuộc sống
-
Toán 8 tập 2 - Kết nối tri thức
Toán 8, giải toán lớp 8 kết nối tri thức với cuộc sống
Bài 12. Hình bình hành Toán 8 kết nối tri thức
Giải bài 3.15 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức
Cho hình bình hành ABCD.
Tổng hợp đề thi giữa kì 2 lớp 8 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên
Đề bài
Cho hình bình hành ABCD. Gọi E, F lần lượt là trung điểm của AB, CD. Chứng minh BF = DE.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng các tính chất của hình bình hành
+ Các cạnh đối bằng nhau
+ Các góc đối bằng nhau
+ Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Lời giải chi tiết
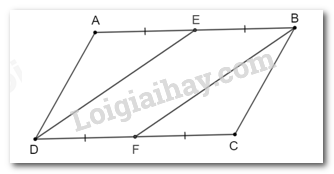
Vì ABCD là hình bình hành nên AB = CD, AB // CD.
Mà E, F lần lượt là trung điểm của AB, CD nên AE = BE, CF = DF.
Do đó AE = BE = CF = DF.
Xét tứ giác BEDF có:
BE = DF (chứng minh trên);
BE // DF (vì AB // CD)
Do đó tứ giác BEDF là hình bình hành.
Suy ra BF = DE (đpcm).
Bình luận
Chia sẻ
- Giải bài 3.16 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.17 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.18 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.14 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức
- Giải bài 3.13 trang 61 SGK Toán 8 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
- Giải dự án 2 trang 112 SGK Toán 8 tập 1
- Lý thuyết Hình chóp tứ giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình chóp tam giác đều SGK Toán 8 - Kết nối tri thức
- Lý thuyết Hình đồng dạng SGK Toán 8 - Kết nối tri thức
- Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Kết nối tri thức
