Toán 8, giải toán lớp 8 Cùng khám phá Bài 3. Hình bình hành - Toán 8 - Cùng khám phá

Giải bài 3.14 trang 66 SGK Toán 8 - Cùng khám phá


Bàn vẽ có hai chân AB và CD được gắn với nhau theo hình chữ X

Đề bài

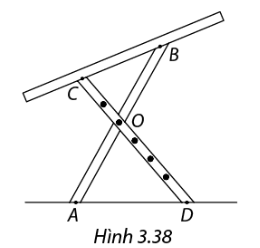
Bàn vẽ có hai chân AB và CD được gắn với nhau theo hình chữ X tại trung điểm O của chân AB. Điểm O có thể di chuyển dọc theo chân bàn CD để điều chỉnh độ nghiêng của mặt bàn (Hình 3.38). Điểm O ở vị trí nào trên đoạn thẳng CD thì cạnh bàn BC song song với đường thẳng AD trên mặt đât? Khi đó ABCD là hình gì?

Phương pháp giải - Xem chi tiết

Sử dụng dấu hiệu nhận biết của hình bình hành:

Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Lời giải chi tiết

Ta thấy AB và CD là hai đường chéo của tứ giác ADBC. Khi O nằm trên trung điểm của CD thì \(BC//AD\) và tứ giác ADBC là hình bình hành (dựa vào dấu hiệu nhận biết).

 


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & lộ trình Up 10! trên Tuyensinh247.com Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua