Bài 3. Giải tam giác và ứng dụng thực tế - SBT Toán 10 ..

Giải bài 3 trang 79 sách bài tập toán 10 - Chân trời sáng tạo

Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng

Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...

Đề bài

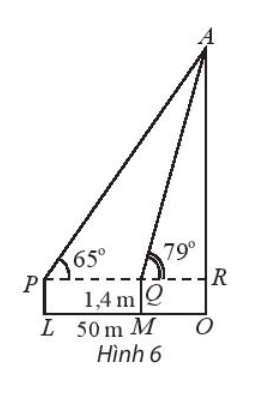
Để xác định chiều cao của một tòa nhà cao tầng, một người đứng tại điểm M, sử dụng giác kế nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {RQA} = 79^\circ \), người đó lùi ra xa một khoảng cách \(LM = 50\) m thì nhìn thấy đỉnh tòa nhà với góc nâng \(\widehat {RPA} = 65^\circ \). Hãy tính chiều cao của tòa nhà, biết rằng khoảng cách từ mặt đất đến ống ngắm của giác kế đó là \(PL = QM = 1,4\) m (hình 6)

Lời giải chi tiết

Ta có chiều cao của nhà cao tầng là \(AO = AR + RO = AR + 1,4\)

Góc \(\widehat {AQR}\) là góc ngoài của tam giác APQ tại đỉnh Q suy ra \(\widehat {AQR} = \widehat {APQ} + \widehat {QAP} \Rightarrow \widehat {QAP} = \widehat {AQR} - \widehat {APQ} = 79^\circ - 65^\circ = 14^\circ \)

Áp dụng định lí sin vào tam giác APQ ta có:

\(\frac{{PQ}}{{\sin \widehat {PAQ}}} = \frac{{AQ}}{{\sin \widehat {APQ}}} = \frac{{50}}{{\sin 14^\circ }} \Rightarrow AQ = \frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ \)

Xét tam giác AQR ta có:

\(\frac{{AR}}{{\sin \widehat {AQR}}} = \frac{{AQ}}{{\sin \widehat {ARQ}}} = \frac{{\frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ }}{{\sin 90^\circ }} \Rightarrow AR = \frac{{\frac{{50}}{{\sin 14^\circ }}.\sin 65^\circ }}{{\sin 90^\circ }}.\sin 79^\circ \simeq 183,87\)

\( \Rightarrow AO \simeq 183,87 + 1,4 = 185,27\)

Vậy tòa nhà cao xấp xỉ 185,27 m

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 trang 79 sách bài tập toán 10 - Chân trời sáng tạo
Một vệ tinh quay quanh Trái Đất, đang bay phía trên hai trạm quan sát ở hai thành phố Hồ Chí Minh và Cần Thơ.
Giải bài 5 trang 79 sách bài tập toán 10 - Chân trời sáng tạo
Tính khoảng cách AB giữa nóc hai tòa cao ốc. Cho biết khoảng cách từ hai điểm đó đến một vệ tinh viễn thông lần lượt là 360 km, 340 km và góc nhìn từ vệ tinh đến A và B
Giải bài 6 trang 79 sách bài tập toán 10 - Chân trời sáng tạo
Một chiếc tàu khởi hành từ bến cảng, đi về hướng Bắc 15km,
Giải bài 2 trang 79 sách bài tập toán 10 - Chân trời sáng tạo
Tính các góc chưa biết của tam giác ABC trong các trường hợp sau:
Giải bài 1 trang 79 sách bài tập toán 10 - Chân trời sáng tạo
Cho tam giác ABC với BC = a;AC = b;AB = c và a = b. Chứng minh rằng: