Giải bài 3 trang 158 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Đề bài

Thâm niên công tác của các công nhân hai nhà máy A và B.

a) Hãy so sánh thâm niên công tác của nhân viên hai nhà máy theo số trung bình và trung vị.

b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của hai mẫu số liệu ghép nhóm trên.

Lời giải chi tiết

a) Bảng tần số ghép nhóm bao gồm giá trị đại diện là:

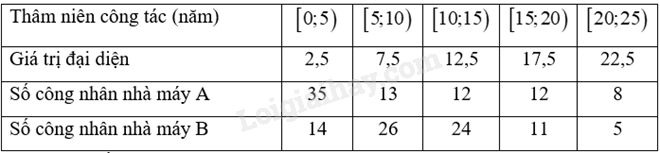
Trung bình số năm thâm niên của công nhân nhà máy A là:

\(\overline {{x_A}}  = \frac{{2,5.35 + 7,5.13 + 12,5.12 + 17,5.12 + 22,5.8}}{{35 + 13 + 12 + 12 + 8}} = 9,0625\) (năm)

Trung bình số năm thâm niên của công nhân nhà máy B là:

\(\overline {{x_B}}  = \frac{{2,5.14 + 7,5.26 + 12,5.24 + 17,5.11 + 22,5.5}}{{14 + 26 + 24 + 11 + 5}} = 10,4375\) (năm)

Vậy nếu so sánh theo số trung bình (năm) thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.

Nhà máy A:

Cỡ mẫu \(n = 80\)

Gọi \({x_1},{x_2},...,{x_{80}}\) là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có: \({x_1},...,{x_{35}} \in \left[ {0;5} \right),{x_{36}},...,{x_{48}} \in \left[ {5;10} \right),{x_{49}},...,{x_{60}} \in \left[ {10;15} \right),\)

\({x_{61}},...,{x_{72}} \in \left[ {15;20} \right),{x_{73}},...,{x_{80}} \in \left[ {20;25} \right)\).

Do cỡ mẫu \(n = 80\) nên trung vị của mẫu số liệu là \(\frac{1}{2}\left( {{x_{40}} + {x_{41}}} \right)\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {5;10} \right)\).

Trung vị của mẫu số liệu ghép nhóm là: \({M_e}\left( A \right) = 5 + \frac{{\frac{{80}}{2} - 35}}{{13}}.\left( {10 - 5} \right) = \frac{{90}}{{13}}\)

Nhà máy B:

Cỡ mẫu \(n = 80\)

Gọi \({x_1},{x_2},...,{x_{80}}\) là mẫu số liệu được xếp theo thứ tự không giảm.

Ta có: \({x_1},...,{x_{14}} \in \left[ {0;5} \right),{x_{15}},...,{x_{40}} \in \left[ {5;10} \right),{x_{41}},...,{x_{64}} \in \left[ {10;15} \right),\)

\({x_{65}},...,{x_{75}} \in \left[ {15;20} \right),{x_{76}},...,{x_{80}} \in \left[ {20;25} \right)\)

Do cỡ mẫu \(n = 80\) nên trung vị của mẫu số liệu là \(\frac{1}{2}\left( {{x_{40}} + {x_{41}}} \right)\). Do \({x_{40}} \in \left[ {5;10} \right),{x_{41}} \in \left[ {10;15} \right)\) nên ta có trung vị là \({M_e}\left( B \right) = 10\)

Vì \(\frac{{90}}{{13}} < 10\) nên nếu so sánh theo trung vị thì thâm niên công tác của nhân viên công ty A ngắn hơn thâm niên công tác của nhân viên công ty B.

b) Nhà máy A:

Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {0;5} \right)\).

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:

\({Q_1}\left( A \right) = 0 + \frac{{\frac{{80}}{4} - 0}}{{35}}.\left( {5 - 0} \right) = \frac{{20}}{7}\)

Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{60}} + {x_{61}}} \right)\). Do \({x_{60}} \in \left[ {10;15} \right),{x_{61}} \in \left[ {15;20} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \({Q_3}\left( A \right) = 15\).

Nhà máy B:

Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ nhất của mẫu số liệu là \(\frac{1}{2}\left( {{x_{20}} + {x_{21}}} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm \(\left[ {5;10} \right)\).

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}\left( B \right) = 5 + \frac{{\frac{{80}}{4} - 14}}{{26}}.\left( {10 - 5} \right) = \frac{{80}}{{13}}\)

Do cỡ mẫu \(n = 80\) nên tứ phân vị thứ ba của mẫu số liệu là \(\frac{1}{2}\left( {{x_{60}} + {x_{61}}} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu thuộc nhóm \(\left[ {10;15} \right)\) nên tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}\left( B \right) = 10 + \frac{{\frac{{3.80}}{4} - \left( {14 + 26} \right)}}{{24}}.\left( {15 - 10} \right) = \frac{{85}}{6}\)