Giải bài 3 (9.34) trang 84 vở thực hành Toán 7 tập 2
Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.
Đề bài
Cho tam giác ABC. Kẻ tia phân giác At của góc tạo bởi tia AB và tia đối của tia AC. Chứng minh rằng nếu đường thẳng chứa tia At song song với đường thẳng BC thì tam giác ABC cân tại A.
Phương pháp giải - Xem chi tiết
+ Gọi tia đối của tia AC là tia Am.
+ Chỉ ra \(\widehat {{A_1}} = \widehat {{A_2}}\), \(\widehat {ABC} = \widehat {{A_2}},\widehat {ACB} = \widehat {{A_1}}\) nên \(\widehat {ABC} = \widehat {ACB}\).
Lời giải chi tiết
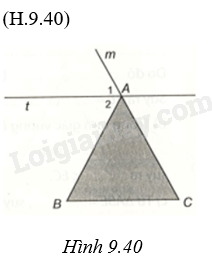
Gọi tia đối của tia AC là Am. Ta có tia At chia góc mAB thành hai góc \(\widehat {{A_1}}\) và \(\widehat {{A_2}}\), \(\widehat {{A_1}} = \widehat {{A_2}}\).
Vì At//BC nên ta có \(\widehat {ABC} = \widehat {{A_2}},\widehat {ACB} = \widehat {{A_1}}\).
Suy ra \(\widehat {ACB} = \widehat {{A_1}} = \widehat {{A_2}} = \widehat {ABC}\). Vậy ABC là tam giác cân tại A.
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục













Danh sách bình luận