Giải bài 3 (9.12) trang 73 vở thực hành Toán 7 tập 2

Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13). a) So sánh MB với (MN + NB), từ đó suy ra (MA + MB < NA + NB). b) So sánh NA với (CA + CN), từ đó suy ra (NA + NB < CA + CB). c) Chứng minh (MA + MB < CA + CB).

Đề bài

Cho điểm M nằm bên trong tam giác ABC. Gọi N là giao điểm của đường thẳng AM và cạnh BC (H.9.13).

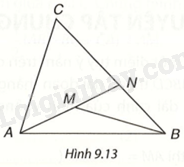
a) So sánh MB với \(MN + NB\), từ đó suy ra \(MA + MB < NA + NB\).

b) So sánh NA với \(CA + CN\), từ đó suy ra \(NA + NB < CA + CB\).

c) Chứng minh \(MA + MB < CA + CB\).

Phương pháp giải - Xem chi tiết

a) Chỉ ra \(MB < MN + NB\), suy ra \(MA + MB < MA + MN + NB = NA + NB\).

b) Chỉ ra \(NA < CA + CN\), suy ra \(NA + NB < CA + NB + CN = CA + CB\).

c) Vì \(MA + MB < NA + NB\), \(NA + NB < CA + CB\) nên \(MA + MB < CA + CB\).

Lời giải chi tiết

a) Trong tam giác MNB ta có \(MB < MN + NB\), do đó

\(MA + MB < MA + MN + NB = NA + NB\) (vì \(MA + MN = NA\))

b) Trong tam giác ACN ta có \(NA < CA + CN\), do đó

\(NA + NB < CA + NB + CN = CA + CB\) (vì \(NB + NC = BC\))

c) Từ a) và b) ta có \(MA + MB < NA + NB\)

\(NA + NB < CA + CB\).

Suy ra \(MA + MB < NA + NB < CA + CB\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Giải bài 4 (9.13) trang 73, 74 vở thực hành Toán 7 tập 2
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh AD nhỏ hơn nửa chu vi tam giác ABC.
Giải bài 5 trang 74 vở thực hành Toán 7 tập 2
Cho tam giác ABC, biết (AB = 3cm,AC = 6cm). Tính độ dài cạnh BC, biết độ dài này là một số nguyên tố.
Giải bài 2 (9.11) trang 73 vở thực hành Toán 7 tập 2
a) Cho tam giác ABC có (AB = 1cm) và (BC = 7cm). Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên (cm). b) Cho tam giác ABC có (AB = 2cm,BC = 6cm) và BC là cạnh lớn nhất. Hãy tìm độ dài cạnh CA biết rằng đó là một số nguyên (cm).
Giải bài 1 (9.10) trang 72 vở thực hành Toán 7 tập 2
Cho các bộ ba đoạn thẳng có độ dài như sau: a) 2cm, 3cm, 5cm. b) 3cm, 4cm, 6cm. c) 2cm, 4cm, 5cm. Hỏi bộ ba nào không thể là độ dài ba cạnh của một tam giác? Vì sao? Với mỗi bộ ba còn lại, hãy vẽ một tam giác có độ dài ba cạnh được cho trong bộ ba đó.
Giải câu hỏi trắc nghiệm trang 71, 72 vở thực hành Toán 7 tập 2
Chọn phương án đúng trong mỗi câu sau: Trong tam giác ABC, ta có: A. (BC > AB + AC). B. (AB + BC < AC). C. (AC > AB + BC). D. (AB < AC + BC).