Giải bài 3 (10.22) trang 102, 103 vở thực hành Toán 7 tập 2

Người ta xếp một số viên gạch dạng hình hộp chữ nhật tạo thành một khối hình lập phương cạnh 20cm như Hình 10.22. a) Tính diện tích xung quanh và diện tích toàn phần của khối gạch hình lập phương. b) Tìm kích thước mỗi viên gạch.

Đề bài

Người ta xếp một số viên gạch dạng hình hộp chữ nhật tạo thành một khối hình lập phương cạnh 20cm như Hình 10.22.

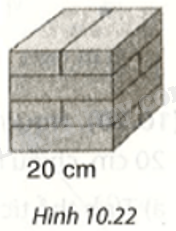
a) Tính diện tích xung quanh và diện tích toàn phần của khối gạch hình lập phương.
b) Tìm kích thước mỗi viên gạch.

Phương pháp giải - Xem chi tiết

a) + Diện tích xung quanh của hình lập phương cạnh a là \({S_{xq}} = 4{a^2}\).

+ Diện tích toàn phần= diện tích xung quanh+ diện tích hai đáy.

b) + Chiều dài của mỗi viên gạch bằng độ dài cạnh hình lập phương.

+ Chiều rộng của mỗi viên gạch= độ dài cạnh hình lập phương: 2.

+ Chiều cao của mỗi viên gạch= độ dài cạnh hình lập phương: 4.

Lời giải chi tiết

a) Diện tích xung quanh của hình lập phương là: \({S_{xq}} = {4.20^2} = 1\;600\left( {c{m^2}} \right)\).

Diện tích toàn phần của hình lập phương là: \({S_{tp}} = 1\;600 + {2.20^2} = 2\;400\left( {c{m^2}} \right)\).

b) Kích thước của mỗi viên gạch:

Chiểu rộng là \(20:2 = 10cm\).

Chiều dài là 20cm.

Chiều cao là \(20:4 = 5\left( {cm} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 4 (10.23) trang 103 vở thực hành Toán 7 tập 2
Một căn phòng dạng hình hộp chữ nhật có chiều dài 5m, chiều rộng 4m và chiều cao 3m. Người ta muốn lăn sơn tường và trần nhà. Hỏi diện tích cần lăn sơn là bao nhiêu mét vuông, biết rằng tổng diện tích các cửa bằng (5,8{m^2})?
Giải bài 5 (10.24) trang 103 vở thực hành Toán 7 tập 2
Một bể cá dạng hình hộp chữ nhật làm bằng kính (không có nắp) có chiều dài 80cm, chiều rộng 50cm, chiều cao 45cm. Mực nước ban đầu trong bể cao 35cm. a) Tính diện tích kính dùng để làm bể cá đó. b) Người ta cho vào bể một hòn đá trang trí chìm hẳn trong nước thì mực nước của bể dâng lên thành 37,5cm. Tính thể tích hòn đá.
Giải bài 6 (10.25) trang 103 vở thực hành Toán 7 tập 2
Một chiếc cốc có dạng hình trụ, chứa đầy nước. Hỏi nếu bỏ vào cốc 5 viên đá dạng hình lập phương có cạnh 2cm thì lượng nước trào ra ngoài là bao nhiêu?
Giải bài 2 (10.21) trang 102 vở thực hành Toán 7 tập 2
Tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lăng trụ trong Hình 10.21.
Giải bài 1 (10.20) trang 101 vở thực hành Toán 7 tập 2
Người ta làm một cái hộp có dạng hình hộp chữ nhật bằng bìa với chiều dài 20cm, chiều rộng 14cm và chiều cao 15cm. a) Tính thể tích của cái hộp. b) Tính diện tích bìa dùng để làm cái hộp.