Toán 8, giải toán lớp 8 cánh diều Bài 4. Tính chất đường phân giác của tam giác Toán 8 cá..

Giải bài 2 trang 69 SGK Toán 8 – Cánh diều


Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt

Đề bài

Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Dựa vào tính chất đường phân giác để chứng minh yêu cầu bài toán.

Lời giải chi tiết

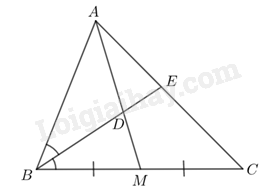
Tam giác ABC có đường phân giác BE nên ta có: \(\frac{{EC}}{{EA}} = \frac{{BC}}{{BA}}\)

Mà M là trung điểm của BC nên \(BC = 2BM\)

\( \Rightarrow \frac{{EC}}{{EA}} = 2\frac{{BM}}{{BA}}\,\,\left( 1 \right)\)

Tam giác ABM có đường phân giác BD nên ta có: \(\frac{{DM}}{{DA}} = \frac{{BM}}{{BA}}\,\,\left( 2 \right)\)

Từ (1) và (2) ta có: \(\frac{{EC}}{{EA}} = 2\frac{{DM}}{{DA}}\).


Bình chọn:
4 trên 11 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store