 Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
 Bài tập cuối chương 9 trang 86, 87, 88, 89 Vở thực hành..
Bài tập cuối chương 9 trang 86, 87, 88, 89 Vở thực hành..
Giải bài 2 (9.37) trang 87 vở thực hành Toán 7 tập 2
Cho tam giác ABC (left( {AB > AC} right)). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, (BD = BA), (CE = CA) (H.9.44). a) So sánh (widehat {ADE}) và (widehat {AED}). b) So sánh các đoạn thẳng AD và AE.
Đề bài
Cho tam giác ABC \(\left( {AB > AC} \right)\). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, \(BD = BA\), \(CE = CA\) (H.9.44).
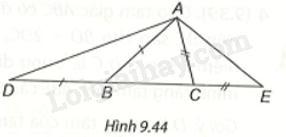
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
Phương pháp giải - Xem chi tiết
a) + Chứng minh \(\widehat {{A_1}} = \widehat D = \frac{1}{2}\widehat {ABC}\), \(\widehat {{A_2}} = \widehat E = \frac{1}{2}\widehat {ACB}\).
+ Vì \(AB > AC\) nên \(\widehat {ACB} > \widehat {ABC}\), suy ra \(\widehat E > \widehat D\).
b) Trong tam giác ADE vì \(\widehat E > \widehat D\) nên \(AD > AE\).
Lời giải chi tiết
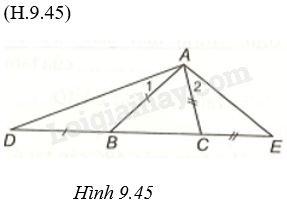
a) Tam giác ABD cân tại B và có góc ngoài đỉnh B là góc ABC nên \(\widehat {{A_1}} = \widehat D = \frac{1}{2}\widehat {ABC}\).
Tam giác ACE cân tại C và có góc ngoài đỉnh C là góc ACB nên \(\widehat {{A_2}} = \widehat E = \frac{1}{2}\widehat {ACB}\).
Do \(AB > AC\) nên \(\widehat {ACB} > \widehat {ABC}\), suy ra \(\frac{1}{2}\widehat {ACB} > \frac{1}{2}\widehat {ABC}\) hay \(\widehat E > \widehat D\).
b) Trong tam giác ADE vì \(\widehat E > \widehat D\) nên \(AD > AE\).
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục












Danh sách bình luận