-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
SBT Toán 10 - giải SBT Toán 10 - Cánh diều
Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụn..
Giải bài 17 trang 48 SBT toán 10 - Cánh diều
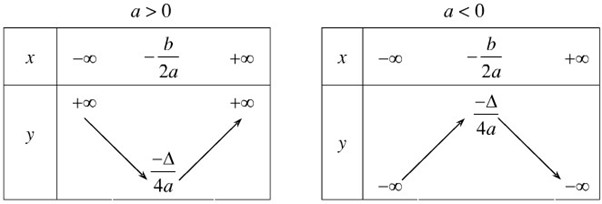
Xác định hàm số bậc 2 biết hệ số tự do (c = 2) và bảng biến thiên tương ứng trong mỗi trường hợp sau:
Tổng hợp đề thi giữa kì 1 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh
Đề bài
Xác định hàm số bậc 2 biết hệ số tự do \(c = 2\) và bảng biến thiên tương ứng trong mỗi trường hợp sau:
Phương pháp giải - Xem chi tiết
Cho hàm số \(y = a{x^2} + bx + c\)
Lời giải chi tiết
Đồ thị hàm số có dạng tổng quát: \(y = f\left( x \right) = a{x^2} + bx + 2\)
a) Đồ thị hàm số có đỉnh I(-1;-2) nên
\(\left\{ \begin{array}{l}x = \frac{{ - b}}{{2a}} = - 1\\f\left( { - 1} \right) = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 2a\\a{\left( { - 1} \right)^2} + b\left( { - 1} \right) + 2 = - 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 2a\\a - b = - 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 4\\b = 8\end{array} \right.\)
Vậy hàm số bậc 2 đó là \(y = 4{x^2} + 8x + 2\)
b) Đồ thị hàm số có đỉnh \(\left\{ \begin{array}{l}x = \frac{{ - b}}{{2a}} = 2\\f\left( 2 \right) = 8\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = - 4a\\a{.2^2} + b.2 + 2 = 8\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b = 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{{ - 3}}{2}\\b = 6\end{array} \right.\)
Vậy hàm số bậc 2 đó là \(y = \frac{{ - 3}}{2}{x^2} + 6x + 2\)
Bình luận
Chia sẻ
- Giải bài 18 trang 48 SBT toán 10 - Cánh diều
- Giải bài 19 trang 48 SBT toán 10 - Cánh diều
- Giải bài 16 trang 48 SBT toán 10 - Cánh diều
- Giải bài 15 trang 47 SBT toán 10 - Cánh diều
- Giải bài 14 trang 47 SBT toán 10 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
