Giải bài 10 trang 95 sách bài tập toán 11 - Chân trời sáng tạo tập 1
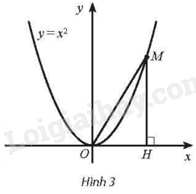
Cho điểm M thay đổi trên parabol \(y = {x^2}\); H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H. Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left( {OM - MH} \right)\)
Đề bài
Cho điểm M thay đổi trên parabol \(y = {x^2}\); H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H. Tìm \(\mathop {\lim }\limits_{x \to + \infty } \left( {OM - MH} \right)\)
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về các phép toán về giới của hàm số tại vô cực để tính: Cho \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = L,\mathop {\lim }\limits_{x \to + \infty } g\left( x \right) = M\), khi đó: \(\mathop {\lim }\limits_{x \to + \infty } \left[ {f\left( x \right) \pm g\left( x \right)} \right] = L \pm M\), \(\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{L}{M}\)
+ Sử dụng kiến thức về giới hạn hữu hạn cơ bản để tính: \(\mathop {\lim }\limits_{x \to + \infty } c = c,\mathop {\lim }\limits_{x \to + \infty } \frac{c}{{{x^k}}} = 0\) (với c là hằng số, k là số nguyên dương)
Lời giải chi tiết
Ta có: \(M\left( {x;{x^2}} \right)\), \(OM = \sqrt {{x^2} + {x^4}} \), \(MH = {x^2}\).
Nên\(\mathop {\lim }\limits_{x \to + \infty } \left( {OM - MH} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + {x^4}} - {x^2}} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}}}{{\sqrt {{x^2} + {x^4}} + {x^2}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{\sqrt {\frac{1}{{{x^2}}} + 1} + 1}} = \frac{1}{2}\).
- Giải bài 11 trang 95 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 12 trang 95 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 9 trang 95 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 8 trang 94 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 7 trang 94 sách bài tập toán 11 - Chân trời sáng tạo tập 1
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 5 trang 162 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 4 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 3 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 2 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 1 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 5 trang 162 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 4 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 3 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 2 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1
- Giải bài 1 trang 161 sách bài tập toán 11 - Chân trời sáng tạo tập 1













Danh sách bình luận