-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
SBT Toán 10 - giải SBT Toán 10 - Cánh diều
Bài 1. Định lí cosin và định lí sin trong tam giác. Giá..
Giải bài 10 trang 75 SBT toán 10 - Cánh diều
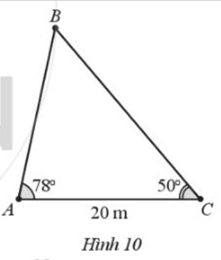
Một cây cao bị nghiêng so với mặt đất góc 780. Từ vị trí C cách gốc cây 20 m, người ta tiến hành đo đạc và thu được kết quả \(\widehat {ACB} = {50^0}\) với B là vị trí ngọn cây (Hình 10).
Đề bài
Một cây cao bị nghiêng so với mặt đất góc 780. Từ vị trí C cách gốc cây 20 m, người ta tiến hành đo đạc và thu được kết quả \(\widehat {ACB} = {50^0}\) với B là vị trí ngọn cây (Hình 10). Tính khoảng cách từ gốc cây (điểm A) đến ngọn cây (điểm B) (làm tròn kết quả đến hàng phần mười theo đơn vị mét)
Phương pháp giải - Xem chi tiết
Tính góc B và sử dụng định lí sin để tính độ dài cạnh AB của ∆ABC rồi kết luận
Lời giải chi tiết
Ta có: \(\widehat B = {180^0} - (\widehat A + \widehat C) = {52^0}\)
Áp dụng định lí sin cho ∆ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} \Rightarrow AB = \frac{{AC.\sin C}}{{\sin B}} = \frac{{20.\sin {{50}^0}}}{{\sin {{52}^0}}} \approx 19,4\)
Vậy khoảng cách từ gốc cây đến ngọn cây là 19,4 m
Bình luận
Chia sẻ
- Giải bài 11 trang 75 SBT toán 10 - Cánh diều
- Giải bài 9 trang 75 SBT toán 10 - Cánh diều
- Giải bài 8 trang 75 SBT toán 10 - Cánh diều
- Giải bài 7 trang 75 SBT toán 10 - Cánh diều
- Giải bài 6 trang 75 SBT toán 10 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Cánh diều - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
