Giải bài 10 trang 128 vở thực hành Toán 9 tập 2

Tính thể tích hình tạo thành khi cho hình bên quay quanh IH một vòng.

Đề bài

Tính thể tích hình tạo thành khi cho hình bên quay quanh IH một vòng.

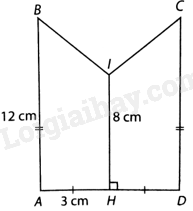
Phương pháp giải - Xem chi tiết

+ Tính thể tích \({V_1}\) của hình trụ có bán kính \(AH = 3cm\), chiều cao \(AB = 12cm\).

+ Tính thể tích \({V_2}\) của hình nón có đường kính \(BC = 6cm\), chiều cao \(h = 12 - 8 = 4\left( {cm} \right)\).

+ Thể tích hình được tạo thành: \(V = {V_1} - {V_2}\)

Lời giải chi tiết

Thể tích hình trụ có bán kính \(AH = 3cm\), chiều cao \(AB = 12cm\) là:

\({V_1} = \pi {.3^2}.12 = 108\pi \left( {c{m^3}} \right)\).

Thể tích hình nón có đường kính đáy \(BC = 6cm\), chiều cao \(h = 12 - 8 = 4cm\) là:

\({V_2} = \frac{1}{3}\pi {.3^2}.4 = 12\pi \left( {c{m^3}} \right)\).

Thể tích của hình tạo thành là:

\(V = {V_1} - {V_2} = 108\pi - 12\pi = 96\pi \left( {c{m^3}} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Giải bài 9 trang 128 vở thực hành Toán 9 tập 2
Nhà hát Cao Văn Lầu và Trung tâm triển lãm Văn hóa Nghệ thuật tỉnh Bạc Liêu có hình dáng ba chiếc nón lá lớn nhất Việt Nam. Tính diện tích mái nhà hình nón có đường kính bằng 45m và chiều cao bằng 24m (làm tròn kết quả đến hàng đơn vị của ({m^2})).
Giải bài 8 trang 127 vở thực hành Toán 9 tập 2
Một chiếc kem ốc quế gồm hai phần: Phần phía dưới là một hình nón có chiều cao gấp đôi bán kính đáy, phần trên là một nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới. Thể tích phần kem phía trên bằng (200c{m^3}). Tính thể tích của cả chiếc kem.
Giải bài 7 trang 127 vở thực hành Toán 9 tập 2
Bạn Khôi cho một cục đá vào một bể nuôi cá hình trụ có đường kính đáy bằng 20cm thì nước trong bể dâng lên 3cm. Hỏi hòn đá cảnh đó có thể tích bao nhiêu?
Giải bài 6 trang 127 vở thực hành Toán 9 tập 2
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn nội tiếp hình vuông A’B’C’D’.
Giải bài 5 trang 126, 127 vở thực hành Toán 9 tập 2
Các hình dưới đây được tạo thành từ các nửa hình cầu, hình trụ và hình nón (có cùng bán kính đáy). Tính thể tích của các hình đó theo kích thước đã cho.
Giải bài 4 trang 126 vở thực hành Toán 9 tập 2
Đèn trời có dạng hình trụ không có một đáy với đường kính đáy bằng 0,8m và thân đèn cao 1m. Tính diện tích giấy dán bên ngoài đèn trời (coi các mép dán không đáng kể).
Giải bài 3 trang 125, 126 vở thực hành Toán 9 tập 2
Quả bóng rổ sử dụng trong thi đấu có dạng hình cầu với đường kính 24cm. Hãy tính: a) Diện tích bề mặt quả bóng. b) Thể tích của quả bóng.
Giải bài 2 trang 125 vở thực hành Toán 9 tập 2
Cho hình nón có bán kính đáy bằng 9cm, độ dài đường sinh bằng 15cm. a) Tính diện tích xung quanh của hình nón. b) Tính thể tích của hình nón. c) Diện tích toàn phần của hình nón bằng tổng diện tích xung quanh và diện tích đáy. Tính diện tích toàn phần của hình nón đã cho.
Giải bài 1 trang 125 vở thực hành Toán 9 tập 2
Cho hình trụ có bán kính đáy bằng 20cm, chiều cao bằng 30cm. a) Tính diện tích xung quanh của hình trụ. b) Tính thể tích của hình trụ.
Giải câu hỏi trắc nghiệm trang 124, 125 vở thực hành Toán 9 tập 2
Khi quay hình chữ nhật ABCD quanh cạnh AB ta được một hình trụ có bán kính đáy bằng độ dài đoạn thẳng: A. AB. B. CD. C. AD. D. AC.