Giải bài 1 (9.14) trang 74 vở thực hành Toán 7 tập 2
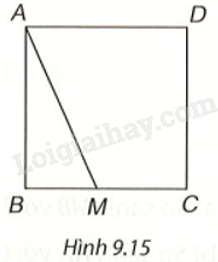
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Đề bài
Hãy giải thích: Nếu M là một điểm tùy ý nằm trên cạnh BC hoặc CD của hình vuông ABCD thì độ dài đoạn thẳng AM luôn lớn hơn hoặc bằng độ dài cạnh của hình vuông đó (H.9.15).
Phương pháp giải - Xem chi tiết
Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.
Lời giải chi tiết
Khi M trùng B (hoặc D) thì AM = a \(\left( {AB = a} \right)\) với a là độ dài cạnh hình vuông. Khi M khác B, M thuộc cạnh BC thì tam giác ABM vuông tại B nên AM là cạnh huyền, do đó \(a = AB < AM\). Tương tự, khi M khác D, M thuộc cạnh CD, ta có $a=AD<AM$.
- Giải bài 2 (9.15) trang 74 vở thực hành Toán 7 tập 2
- Giải bài 3 (9.16) trang 74 vở thực hành Toán 7 tập 2
- Giải bài 4 (9.17) trang 74, 75 vở thực hành Toán 7 tập 2
- Giải bài 5 (9.18) trang 75 vở thực hành Toán 7 tập 2
- Giải bài 6 trang 75 vở thực hành Toán 7 tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục













Danh sách bình luận