Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 3 - Thanh Hóa
I. Phần trắc nghiệm
Đề bài
Họ tất cả các nghiệm của phương trình cosx = 0 là
-
A.
\(x = \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\)
-
B.
\(x = k2\pi \) \((k \in \mathbb{Z})\)
-
C.
\(x = \frac{\pi }{2} + k2\pi \) \((k \in \mathbb{Z})\)
-
D.
\(x = k\pi \) \((k \in \mathbb{Z})\)
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội q = 2. Giá trị của \({u_2}\) bằng
-
A.
8
-
B.
9
-
C.
6
-
D.
\(\frac{3}{2}\)
Đạo hàm của hàm số \(y = {13^x}\) là
-
A.
\(y' = \frac{{{{13}^x}}}{{\ln 13}}\)
-
B.
\(y' = x{.13^{x - 1}}\)
-
C.
\(y' = {13^x}\ln 13\)
-
D.
\(y' = {13^x}\)
-
A.
\({45^o}\)
-
B.
\({60^o}\)
-
C.
\({30^o}\)
-
D.
\({90^o}\)
-
A.
\((1;1)\)
-
B.
\((0;1)\)
-
C.
\((4; + \infty )\)
-
D.
\(( - \infty ;2)\)
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{3x + 2}}{{x - 2}}\) là đường thẳng có phương trình
-
A.
x = 2
-
B.
x = -1
-
C.
x = 3
-
D.
x = -2
Trong không gian Oxy, cho điểm A(1;2;-3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
-
A.
(0;2;-3)
-
B.
(1;0;-3)
-
C.
(1;2;0)
-
D.
(1;0;0)
Trong không gian Oxy, cho hai vecto \(\overrightarrow u = (1;3; - 2)\) và \(\overrightarrow v = (2;1; - 1)\). Tọa độ của vecto \(\overrightarrow u - \overrightarrow v \) là
-
A.
(3;4;-3)
-
B.
(-1;2;-3)
-
C.
(-1;2;-1)
-
D.
(1;-2;1)
Cho hình lập phương ABCD.A’B’C’D’. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
-
A.
\(\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
B.
\(\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
C.
\(\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
D.
\(\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
Một mẫu số liệu ghép nhóm có tứ phân vị là \({Q_1} = 3\), \({Q_2} = 5\), \({Q_3} = 9\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
-
A.
2
-
B.
4
-
C.
5
-
D.
6
Khảo sát thời gian chơi thể thao trong một ngày của 42 học sinh được cho trong bảng sau (thời gian đơn vị phút):

Phương sai của mẫu số liệu (được làm tròn đến hàng đơn vị) bằng
-
A.
598
-
B.
597
-
C.
2477
-
D.
256
\(\int {\left( {\sin x + 4{x^3}} \right)dx} \) bằng
-
A.
\( - \cos x + 4{x^4} + C\)
-
B.
\(\cos x + {x^4} + C\)
-
C.
\(\cos x + 12{x^2} + C\)
-
D.
\( - \cos x + {x^4} + C\)
Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi v(t) = 5 + 3t (m/s), với t là thời gian kể từ khi máy bay bắt đầu chạy đà. Sau 32 giây thì máy bay cất cánh trên đường băng. Gọi s(t) là quãng đường máy bay di chuyển được sau t giây kể từ lúc bắt đầu chạy đà.
a) v(t) = s’(t).
b) \(s(t) = \frac{3}{2}{t^2} + 5t + 5\).
c) Quãng đường máy bay di chuyển được sau 4 giây kể từ khi bắt đầu chạy đà là 49 mét.
d) Quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường băng là 1696 mét.
Trong không gian với hệ tọa độ Oxyz, cho với A(1;-3;3), B(2;-4;5), C(3;-2;1).
a) \(\overrightarrow {AB} = ( - 1;1; - 2)\).
b) Điểm G(a;b;c) là trọng tâm của \(\Delta ABC\) thì a + b + c = 2.
c) Điểm I(xy;z) thỏa mãn \(2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \), khi đó 2x + y + z = 4.
d) Gọi M(x;y;z) là điểm trên mặt phẳng tọa độ (Oyz) sao cho biểu thức \(P = - 2M{A^2} - M{B^2} - 3M{C^2}\) đạt giá trị lớn nhất. Khi đó x + y – z < -5.
a) Hàm số đồng biến trên khoảng (1;5).
b) Hàm số đạt cực đại tại điểm x = 2.
c) a > 0.
d) Phương trình 2f(x) – e = 0 luôn có một nghiệm âm.
Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}\) có đồ thị là đường cong (C). Giả sử A, B là hai điểm thuộc hai nhánh và AB đi qua tâm đối xứng của (C).
a) Tâm đối xứng của (C) là điểm I(1;-1).
b) Hàm số nghịch biến trên khoảng \(( - \infty ;1)\).
c) Có 1 tiếp tuyến của đồ thị (C) song song với đường thẳng \(d:y = - 2x - 1\).
d) Giá trị nhỏ nhất của đoạn thẳng AB bằng \(3\sqrt 2 \).
Trong đợt kiểm tra cuối học kì I lớp 12 của các trường trung học phổ thông, thống kê cho thấy có 80% học sinh tỉnh X đạt yêu cầu; 90% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y . Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu (viết kết quả dưới dạng số thập phân).
Đáp án:
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 1}}\) có đồ thị (C). Gọi d là khoảng cách giữa hai điểm cực trị của (C) và \({d_1}\) là khoảng cách từ điểm cực đại của (C) đến gốc tọa độ. Giá trị của \({d^2} + {d_1}^2\) bằng bao nhiêu?
Đáp án:
Một sọt đựng đồ có dạng hình chóp cụt đều như hình vẽ dưới. Đáy và miệng sọt là các hình vuông có cạnh tương ứng bằng 80 cm và 60 cm. Cạnh bên của sọt dài 50 cm. Tính thể tích của sọt theo đơn vị mét khối, lấy kết quả đến hàng phần trăm.

Đáp án:
Để cái thang có thể tựa vào tường và mặt đất, ngang qua cột đỡ cao 4 m, song song và cách tường 0,5 m kể từ gốc của cột đỡ như hình vẽ thì chiều dài bé nhất của cái thang là \(\sqrt {\frac{a}{b}} \), biết \(\frac{a}{b}\) là phân số tối giản và \(a,b \in {\mathbb{N}^*}\). Khi đó a + 5b bằng bao nhiêu?
Đáp án:
Một chiếc đèn trang trí (gồm các bóng đèn gắn vào một giá hình tròn) như hình bên dưới. Đèn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên giá sao cho tam giác ABC đều. Độ dài của ba đoạn dây OA, OB, OC đều bằng L, trọng lượng của chiếc đèn là 27 N, bán kính của giá hình tròn là 0,5 m.

Biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 12 N . Hỏi chiều dài tối thiểu của mỗi sợi dây là bao nhiêu mét (kết quả làm tròn đến hàng phần trăm)?
Đáp án:
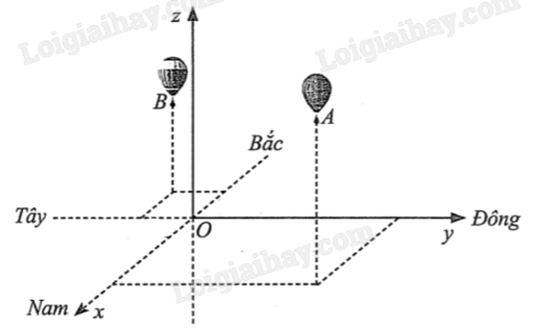
Hai chiếc khinh khí cầu A và B bay lên từ cùng một vị trí O trên mặt đất. Sau một khoảng thời gian, khinh khí cầu A nằm cách điểm xuất phát 4 km về phía Đông và 3km về phía Nam, đồng thời cách mặt đất 1 km; khinh khí cầu B nằm cách điểm xuất phát 1 km về phía Bắc và 1,5 km về phía Tây, đồng thời cách mặt đất 0,8 km (hình minh họa bên dưới). Cùng thời điểm đó, một người đứng trên mặt đất và nhìn thấy hai khinh khí cầu nói trên. Biết rằng, so với các vị trí quan sát khác trên mặt đất, vị trí người đó đứng có tổng khoảng cách đến hai khinh khí cầu là nhỏ nhất. Hỏi tổng khoảng cách nhỏ nhất ấy bằng bao nhiêu kilômét (làm tròn kết quả đến hàng phần trăm)?
Đáp án:
Lời giải và đáp án
Họ tất cả các nghiệm của phương trình cosx = 0 là
-
A.
\(x = \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\)
-
B.
\(x = k2\pi \) \((k \in \mathbb{Z})\)
-
C.
\(x = \frac{\pi }{2} + k2\pi \) \((k \in \mathbb{Z})\)
-
D.
\(x = k\pi \) \((k \in \mathbb{Z})\)
Đáp án : A
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản.
\(\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\).
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3\) và công bội q = 2. Giá trị của \({u_2}\) bằng
-
A.
8
-
B.
9
-
C.
6
-
D.
\(\frac{3}{2}\)
Đáp án : C
Áp dụng công thức số hạng tổng quát của cấp số nhân: \({u_n} = {u_1}.{q^{n - 1}}\).
\({u_2} = {u_1}.q = 3.2 = 6\).
Đạo hàm của hàm số \(y = {13^x}\) là
-
A.
\(y' = \frac{{{{13}^x}}}{{\ln 13}}\)
-
B.
\(y' = x{.13^{x - 1}}\)
-
C.
\(y' = {13^x}\ln 13\)
-
D.
\(y' = {13^x}\)
Đáp án : C
Áp dụng quy tắc tính đạo hàm của hàm số mũ: \(({a^x})' = {a^x}\ln a\).
\(y' = \left( {{{13}^x}} \right) = {13^x}\ln 13\).
-
A.
\({45^o}\)
-
B.
\({60^o}\)
-
C.
\({30^o}\)
-
D.
\({90^o}\)
Đáp án : D
Đưa về tính góc giữa hai đường thẳng.
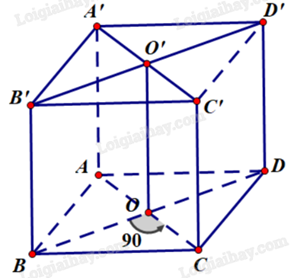
Gọi O là giao điểm của AC và BD, O’ là giao điểm của A’C’ và B’D’.
Ta có OO’ là giao tuyến của hai mặt phẳng (BDD’B’) và (ACC’A’) vì O, O’ cùng thuộc cả hai mặt phẳng trên.
Vì ABCD.A’B’C’D’ là hình lập phương nên dễ dàng chứng minh \(OO' \bot (ABCD) \Rightarrow \left\{ \begin{array}{l}OO' \bot BO\\OO' \bot CO\end{array} \right.\).
Ta có: \(\left\{ \begin{array}{l}BO \subset (BDD'B')\\CO \subset (ACC'A')\\BO \bot OO'\\CO \bot OO'\\OO' \subset (BDD'B') \cap (ACC'A')\end{array} \right.\) suy ra góc giữa hai mặt phẳng (BDD’B’) và (ACC’A’) là góc giữa hai đường thẳng BO và CO, hay BD và AC.
Vì ABCD là hình vuông nên \(AC \bot BD\).
Vậy góc giữa hai mặt phẳng (BDD’B’) và (ACC’A’) bằng \({90^o}\).
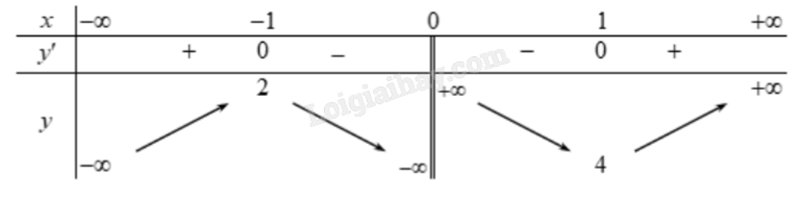
-
A.
\((1;1)\)
-
B.
\((0;1)\)
-
C.
\((4; + \infty )\)
-
D.
\(( - \infty ;2)\)
Đáp án : B
Quan sát bảng biến thiên và nhận xét.
Hàm số nghịch biến trên khoảng (0;1) vì hàm số liên tục và có y’ < 0 trên khoảng đó.
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{3x + 2}}{{x - 2}}\) là đường thẳng có phương trình
-
A.
x = 2
-
B.
x = -1
-
C.
x = 3
-
D.
x = -2
Đáp án : A
Đồ thị hàm số dạng \(y = \frac{{ax + b}}{{cx + d}}\) có đường tiệm cận đứng là \(x = \frac{{ - d}}{c}\).
Tiệm cận đứng của đồ thị hàm số \(y = \frac{{3x + 2}}{{x - 2}}\) là đường thẳng có phương trình x = 2.
Trong không gian Oxy, cho điểm A(1;2;-3). Hình chiếu vuông góc của A lên mặt phẳng (Oxy) có tọa độ là
-
A.
(0;2;-3)
-
B.
(1;0;-3)
-
C.
(1;2;0)
-
D.
(1;0;0)
Đáp án : C
Hình chiếu A’ của điểm A(a;b;c) trên mặt phẳng (Oxy) có tọa độ (a;b;0).
Hình chiếu vuông góc của A(1;2;-3) lên mặt phẳng (Oxy) có tọa độ là (1;2;0).
Trong không gian Oxy, cho hai vecto \(\overrightarrow u = (1;3; - 2)\) và \(\overrightarrow v = (2;1; - 1)\). Tọa độ của vecto \(\overrightarrow u - \overrightarrow v \) là
-
A.
(3;4;-3)
-
B.
(-1;2;-3)
-
C.
(-1;2;-1)
-
D.
(1;-2;1)
Đáp án : C
\(\overrightarrow u - \overrightarrow v = ({x_u} - {x_v};{y_u} - {y_v};{z_u} - {z_v})\).
\(\overrightarrow u - \overrightarrow v = (1 - 2;3 - 1; - 2 + 1) = ( - 1;2; - 1)\).
Cho hình lập phương ABCD.A’B’C’D’. Gọi O là tâm của hình lập phương. Khẳng định nào sau đây là đúng?
-
A.
\(\overrightarrow {AO} = \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
B.
\(\overrightarrow {AO} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
C.
\(\overrightarrow {AO} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
-
D.
\(\overrightarrow {AO} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\)
Đáp án : B
Áp dụng quy tắc hình hộp.
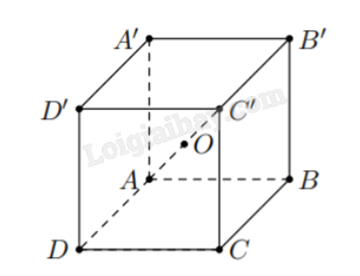
Áp dụng quy tắc hình hộp, ta có: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
Vì O là trung điểm của AC’ nên \(\overrightarrow {AO} = \frac{1}{2}\overrightarrow {AC'} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} } \right)\).
Một mẫu số liệu ghép nhóm có tứ phân vị là \({Q_1} = 3\), \({Q_2} = 5\), \({Q_3} = 9\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm là
-
A.
2
-
B.
4
-
C.
5
-
D.
6
Đáp án : D
Khoảng tứ phân vị của mẫu số liệu ghép nhóm được tính bởi công thức: \({\Delta _Q} = {Q_3} - {Q_1}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \({\Delta _Q} = {Q_3} - {Q_1} = 9 - 3 = 6\).
Khảo sát thời gian chơi thể thao trong một ngày của 42 học sinh được cho trong bảng sau (thời gian đơn vị phút):

Phương sai của mẫu số liệu (được làm tròn đến hàng đơn vị) bằng
-
A.
598
-
B.
597
-
C.
2477
-
D.
256
Đáp án : A
Tính số trung bình của mẫu số liệu, sau đó tính áp dụng công thức tính phương sai.
Trung bình thời gian chơi thể thao trong một ngày của một học sinh là:
\(\overline x = \frac{{10.5 + 30.9 + 50.12 + 70.10 + 90.6}}{{42}} = \frac{{360}}{7}\).
Phương sai của mẫu số liệu là:
\({S^2} = \frac{{{{10}^2}.5 + {{30}^2}.9 + {{50}^2}.12 + {{70}^2}.10 + {{90}^2}.6}}{{42}} - {\left( {\frac{{360}}{7}} \right)^2} = \frac{{29300}}{{49}} \approx 598\).
\(\int {\left( {\sin x + 4{x^3}} \right)dx} \) bằng
-
A.
\( - \cos x + 4{x^4} + C\)
-
B.
\(\cos x + {x^4} + C\)
-
C.
\(\cos x + 12{x^2} + C\)
-
D.
\( - \cos x + {x^4} + C\)
Đáp án : D
Áp dụng quy tắc tính nguyên hàm của hàm số lũy thừa và hàm số lượng giác:
\(\int {{x^\alpha }dx} = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}\); \(\int {\sin xdx} = - \cos x + C\).
\(\int {\left( {\sin x + 4{x^3}} \right)dx} = - \cos x + {x^4} + C\).
Một máy bay di chuyển ra đến đường băng và bắt đầu chạy đà để cất cánh. Giả sử vận tốc của máy bay khi chạy đà được cho bởi v(t) = 5 + 3t (m/s), với t là thời gian kể từ khi máy bay bắt đầu chạy đà. Sau 32 giây thì máy bay cất cánh trên đường băng. Gọi s(t) là quãng đường máy bay di chuyển được sau t giây kể từ lúc bắt đầu chạy đà.
a) v(t) = s’(t).
b) \(s(t) = \frac{3}{2}{t^2} + 5t + 5\).
c) Quãng đường máy bay di chuyển được sau 4 giây kể từ khi bắt đầu chạy đà là 49 mét.
d) Quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường băng là 1696 mét.
a) v(t) = s’(t).
b) \(s(t) = \frac{3}{2}{t^2} + 5t + 5\).
c) Quãng đường máy bay di chuyển được sau 4 giây kể từ khi bắt đầu chạy đà là 49 mét.
d) Quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường băng là 1696 mét.
a) Áp dụng lý thuyết ý nghĩa cơ học của đạo hàm.
b) Tìm \(s(t) = \int {v(t)dt} \).
c) Tính s(4).
d) Tính s(32).
a) Đúng. Từ ý nghĩa cơ học của đạo hàm, ta có v(t) = s’(t).
b) Sai. Ta có v(t) = s’(t) nên \(s(t) = \int {v(t)dt} = \int {(5 + 3t)dt} = \frac{3}{2}{t^2} + 5t + C\).
Theo đề bài, t là thời gian kể từ khi máy bay bắt đầu chạy đà. Do đó, khi t = 0, máy bay chỉ mới bắt đầu di chuyển, tức \(s(0) = 0 \Rightarrow \frac{3}{2}{.0^2} + 5.0 + C = 0 \Rightarrow C = 0\).
Vậy \(s(t) = \frac{3}{2}{t^2} + 5t\).
c) Sai. Ta có \(s(4) = \frac{3}{2}{.4^2} + 5.4 = 44\) (m).
d) Đúng. \(s(32) = \frac{3}{2}{.32^2} + 5.32 = 1696\) (m).
Vậy quãng đường máy bay đã di chuyển từ khi bắt đầu chạy đà đến khi rời đường băng (trong khoảng thời gian 32 giây) là 1696 m.
Trong không gian với hệ tọa độ Oxyz, cho với A(1;-3;3), B(2;-4;5), C(3;-2;1).
a) \(\overrightarrow {AB} = ( - 1;1; - 2)\).
b) Điểm G(a;b;c) là trọng tâm của \(\Delta ABC\) thì a + b + c = 2.
c) Điểm I(xy;z) thỏa mãn \(2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \), khi đó 2x + y + z = 4.
d) Gọi M(x;y;z) là điểm trên mặt phẳng tọa độ (Oyz) sao cho biểu thức \(P = - 2M{A^2} - M{B^2} - 3M{C^2}\) đạt giá trị lớn nhất. Khi đó x + y – z < -5.
a) \(\overrightarrow {AB} = ( - 1;1; - 2)\).
b) Điểm G(a;b;c) là trọng tâm của \(\Delta ABC\) thì a + b + c = 2.
c) Điểm I(xy;z) thỏa mãn \(2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \), khi đó 2x + y + z = 4.
d) Gọi M(x;y;z) là điểm trên mặt phẳng tọa độ (Oyz) sao cho biểu thức \(P = - 2M{A^2} - M{B^2} - 3M{C^2}\) đạt giá trị lớn nhất. Khi đó x + y – z < -5.
a, b, c) Sử dụng các biểu thức tọa độ trong không gian.
d) Ứng dụng tọa độ điểm I vừa tìm ở câu c).
a) Sai. \(\overrightarrow {AB} = (2 - 1; - 4 + 3;5 - 3) = (1; - 1;2)\).
b) Đúng. \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 + 2 + 3}}{3} = 2\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{ - 3 - 4 - 2}}{3} = - 3\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{3 + 5 + 1}}{3} = 3\end{array} \right. \Rightarrow G(2; - 3;3)\)
\(\Rightarrow a + b + c = 2 - 3 + 3 = 2\).
c) Đúng. Ta có:
\(\overrightarrow {IA} = (1 - x;-3 - y;3 - z)\), \(\overrightarrow {IB} = (2 - x; - 4 - y;5 - z)\), \(\overrightarrow {IC} = (3 - x; - 2 - y;1 - z)\).
\(2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \Leftrightarrow \left\{ \begin{array}{l}13 - 6x = 0\\ - 16 - 6y = 0\\14 - 6z = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{13}}{6}\\y = \frac{{ - 8}}{3}\\z = \frac{7}{3}\end{array} \right. \Rightarrow 2x + y + z = 4\).
d) Sai. Gọi điểm I thỏa mãn \(2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} = \overrightarrow 0 \), theo câu c) ta có \(I\left( {\frac{{13}}{6};\frac{{ - 8}}{3};\frac{7}{3}} \right)\).
Ta có: \( - P = 2M{A^2} + M{B^2} + 3M{C^2} = 2{\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + 3{\overrightarrow {MC} ^2}\)
\( = 2{\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {MI} + \overrightarrow {IB} } \right)^2} + 3{\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)^2}\)
\( = 2\left( {{{\overrightarrow {MI} }^2} + 2\overrightarrow {MI} .\overrightarrow {IA} + {{\overrightarrow {IA} }^2}} \right) + \left( {{{\overrightarrow {MI} }^2} + 2\overrightarrow {MI} .\overrightarrow {IB} + {{\overrightarrow {IB} }^2}} \right) + 3\left( {{{\overrightarrow {MI} }^2} + 2\overrightarrow {MI} .\overrightarrow {IC} + {{\overrightarrow {IC} }^2}} \right)\)
\( = 2{\overrightarrow {MI} ^2} + 4\overrightarrow {MI} .\overrightarrow {IA} + 2{\overrightarrow {IA} ^2} + {\overrightarrow {MI} ^2} + 2\overrightarrow {MI} .\overrightarrow {IB} + {\overrightarrow {IB} ^2} + 3{\overrightarrow {MI} ^2} + 6\overrightarrow {MI} .\overrightarrow {IC} + 3{\overrightarrow {IC} ^2}\)
\( = 6{\overrightarrow {MI} ^2} + 2{\overrightarrow {IA} ^2} + {\overrightarrow {IB} ^2} + 3{\overrightarrow {IC} ^2} + 4\overrightarrow {MI} .\overrightarrow {IA} + 2\overrightarrow {MI} .\overrightarrow {IB} + 6\overrightarrow {MI} .\overrightarrow {IC} \)
\( = 6M{I^2} + 2I{A^2} + I{B^2} + 3I{C^2} + 2\overrightarrow {MI} \left( {2\overrightarrow {IA} + \overrightarrow {IB} + 3\overrightarrow {IC} } \right)\)
\( = 6M{I^2} + 2I{A^2} + I{B^2} + 3I{C^2} + 2\overrightarrow {MI} .\overrightarrow 0 \)
\( = 6M{I^2} + 2I{A^2} + I{B^2} + 3I{C^2}\).
Suy ra \(P = - 6M{I^2} - 2I{A^2} - I{B^2} - 3I{C^2}\).
Do giá trị của \( - 2I{A^2} - I{B^2} - 3I{C^2}\) không đổi nên P đạt giá trị lớn nhất khi và chỉ khi \(M{I^2}\) nhỏ nhất, hay MI nhỏ nhất.
Vì M nằm trên mặt phẳng (Oyz) nên IM nhỏ nhất khi và chỉ khi M là hình chiếu vuông góc của I lên mặt phẳng (Oyz).
Khi đó, \(M\left( {0;\frac{{ - 8}}{3};\frac{7}{3}} \right) \Rightarrow x + y - z = - 5\).
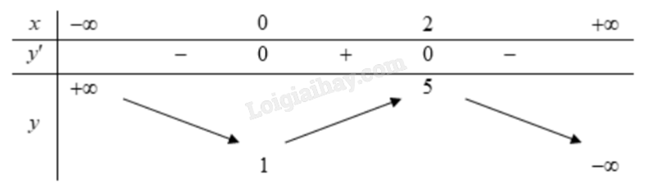
a) Hàm số đồng biến trên khoảng (1;5).
b) Hàm số đạt cực đại tại điểm x = 2.
c) a > 0.
d) Phương trình 2f(x) – e = 0 luôn có một nghiệm âm.
a) Hàm số đồng biến trên khoảng (1;5).
b) Hàm số đạt cực đại tại điểm x = 2.
c) a > 0.
d) Phương trình 2f(x) – e = 0 luôn có một nghiệm âm.
Quan sát bảng biến thiên và nhận xét.
Áp dụng kiến thức về sự tương giao đồ thị.
a) Sai. Hàm số đồng biến trên khoảng (1;2) và nghịch biến trên khoảng (2;5).
b) Đúng. Hàm số đạt cực đại tại điểm x = 2.
c) Sai. Vì \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \) nên hệ số a < 0.
d) Đúng. \(2f(x) - e = 0 \Leftrightarrow f(x) = \frac{e}{2}\).
Phương trình 2f(x) – e = 0 luôn có một nghiệm âm khi đồ thị hàm số y = f(x) cắt đồ thị hàm số \(y = \frac{e}{2}\) tại một điểm có hoành độ âm.
Đồ thị hàm số \(y = \frac{e}{2}\) là đường thẳng song song với trục hoành, được minh họa trên bảng biến thiên như sau:
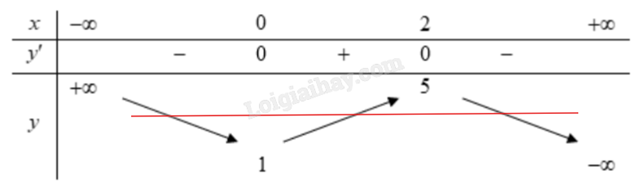
Ta thấy đường thẳng \(y = \frac{e}{2}\) cắt đồ thị y = f(x) tại một điểm có hoành độ âm nên phương trình 2f(x) – e = 0 có một nghiệm âm.
Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}\) có đồ thị là đường cong (C). Giả sử A, B là hai điểm thuộc hai nhánh và AB đi qua tâm đối xứng của (C).
a) Tâm đối xứng của (C) là điểm I(1;-1).
b) Hàm số nghịch biến trên khoảng \(( - \infty ;1)\).
c) Có 1 tiếp tuyến của đồ thị (C) song song với đường thẳng \(d:y = - 2x - 1\).
d) Giá trị nhỏ nhất của đoạn thẳng AB bằng \(3\sqrt 2 \).
a) Tâm đối xứng của (C) là điểm I(1;-1).
b) Hàm số nghịch biến trên khoảng \(( - \infty ;1)\).
c) Có 1 tiếp tuyến của đồ thị (C) song song với đường thẳng \(d:y = - 2x - 1\).
d) Giá trị nhỏ nhất của đoạn thẳng AB bằng \(3\sqrt 2 \).
a) Tâm đối xứng của đồ thị (C) là giao điểm của đường tiệm cận đứng và đường tiệm cận ngang.
b) Xét dấu đạo hàm y’.
c) Từ đường thẳng d, tìm được hệ số góc của tiếp tuyến, từ đó suy ra phương trình tiếp tuyến.
d) Khi AB ngắn nhất, I là trung điểm của AB.
Áp dụng công thức tính khoảng cách giữa hai điểm và bất đẳng thức Cauchy.
a) Sai. Đồ thị (C) có đường tiệm cận đứng là x = 1 và đường tiệm cận ngang là y = 1 nên tâm đối xứng là I(1;1).
b) Đúng. Ta có \(y' = - \frac{2}{{{{(x - 1)}^2}}} < 0\), \(\forall x \ne 1\) nên hàm số nghịch biến trên khoảng \(( - \infty ;1)\).
c) Đúng. Giả sử \(M({x_0};{y_0})\) là tiếp điểm. Tiếp tuyến song song với đường thẳng \(d:y = - 2x - 1\) nên hệ số góc là k = -2.
Khi đó \(y'({x_0}) = - 2 \Leftrightarrow - \frac{2}{{{{({x_0} - 1)}^2}}} = - 2 \Leftrightarrow \left[ \begin{array}{l}{x_0} = 0\\{x_0} = 2\end{array} \right. \Rightarrow \left[ \begin{array}{l}M(0; - 1)\\M(2;3)\end{array} \right.\).
+ Phương trình tiếp tuyến tại M(0;-1) là y = -2x – 1 (loại vì trùng với d).
+ Phương trình tiếp tuyến tại M(2;3) là y = -2(x – 2) + 3 hay y = -2x + 7 (thỏa mãn).
d) Sai. Ta có \(y = \frac{{x + 1}}{{x - 1}} = 1 + \frac{2}{{x - 1}}\).
Khi đó \(A\left( {{x_A};1 + \frac{2}{{{x_A} - 1}}} \right)\), \(B\left( {{x_B};1 + \frac{2}{{{x_B} - 1}}} \right)\).
Khi AB ngắn nhất, I là trung điểm của AB. Do đó:
\(\frac{{{x_A} + {x_B}}}{2} = {x_I} \Leftrightarrow {x_A} + {x_B} = 2{x_I} \Leftrightarrow {x_B} = 2{x_I} - {x_A} = 2.1 - {x_A} = 2 - {x_A}\).
Ta có \(AB = \sqrt {{{({x_B} - {x_A})}^2} + {{({y_B} - {y_A})}^2}} \)
\( = \sqrt {{{({x_B} - {x_A})}^2} + {{\left( {1 + \frac{2}{{{x_B} - 1}} - 1 - \frac{2}{{{x_A} - 1}}} \right)}^2}} \)
\( = \sqrt {{{(2 - {x_A} - {x_A})}^2} + {{\left( {\frac{2}{{2 - {x_A} - 1}} - \frac{2}{{{x_A} - 1}}} \right)}^2}} \)
\( = \sqrt {{{(2 - 2{x_A})}^2} + {{\left( {\frac{2}{{1 - {x_A}}} - \frac{2}{{{x_A} - 1}}} \right)}^2}} \)
\( = \sqrt {{{\left[ {2(1 - {x_A})} \right]}^2} + {{\left( {\frac{2}{{1 - {x_A}}} + \frac{2}{{1 - {x_A}}}} \right)}^2}} \)
\( = \sqrt {4{{(1 - {x_A})}^2} + {{\left( {\frac{4}{{1 - {x_A}}}} \right)}^2}} \)
\( = \sqrt {4{{(1 - {x_A})}^2} + \frac{{16}}{{{{\left( {1 - {x_A}} \right)}^2}}}} \).
Ta có \(4{(1 - {x_A})^2} + \frac{{16}}{{{{\left( {1 - {x_A}} \right)}^2}}} \ge 2\sqrt {4{{(1 - {x_A})}^2}.\frac{{16}}{{{{\left( {1 - {x_A}} \right)}^2}}}} = 2\sqrt {4.16} = 16\).
Do đó \(AB \ge \sqrt {16} = 4\).
Trong đợt kiểm tra cuối học kì I lớp 12 của các trường trung học phổ thông, thống kê cho thấy có 80% học sinh tỉnh X đạt yêu cầu; 90% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y . Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu (viết kết quả dưới dạng số thập phân).
Đáp án:
Đáp án:
Áp dụng quy tắc nhân và phương pháp tính xác suất của biến cố đối.
A: “Có ít nhất một trong hai học sinh được chọn đạt yêu cầu”.
\(\overline A \): “Hai học sinh được chọn không ai đạt yêu cầu”.
Từ đề bài, ta suy ra 20% học sinh tỉnh X không đạt yêu cầu và 10% học sinh tỉnh Y không đạt yêu cầu.
Do đó \(P(\overline A ) = 20\% .10\% = 0,02\).
Vậy \(P(A) = 1 - P(\overline A ) = 1 - 0,02 = 0,98\).
Cho hàm số \(y = \frac{{{x^2} + 3x + 3}}{{x + 1}}\) có đồ thị (C). Gọi d là khoảng cách giữa hai điểm cực trị của (C) và \({d_1}\) là khoảng cách từ điểm cực đại của (C) đến gốc tọa độ. Giá trị của \({d^2} + {d_1}^2\) bằng bao nhiêu?
Đáp án:
Đáp án:
Lập bảng biến thiên, tìm tọa độ các điểm cực trị và áp dụng công thức tính khoảng cách giữa hai điểm.
Ta có \(y' = 1 - \frac{1}{{{{(x + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\).
Ta có bảng biến thiên:
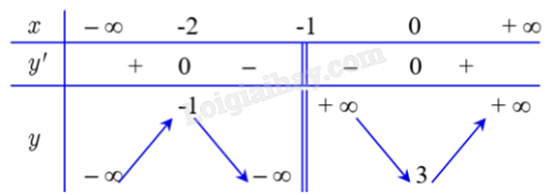
Hai điểm cực trị của (C) là A(0;3) và B(-2;-1) nên \(d = AB = \sqrt {{{( - 2 - 0)}^2} + {{( - 1 - 3)}^2}} = 2\sqrt 5 \Rightarrow {d^2} = 20\).
Điểm cực đại là B(-2;-1) nên \({d_1} = OB = \sqrt {{{( - 2 - 0)}^2} + {{( - 1 - 0)}^2}} = \sqrt 5 \Rightarrow {d_1}^2 = 5\).
Vậy \({d^2} + {d_1}^2 = 20 + 5 = 25\).
Một sọt đựng đồ có dạng hình chóp cụt đều như hình vẽ dưới. Đáy và miệng sọt là các hình vuông có cạnh tương ứng bằng 80 cm và 60 cm. Cạnh bên của sọt dài 50 cm. Tính thể tích của sọt theo đơn vị mét khối, lấy kết quả đến hàng phần trăm.

Đáp án:
Đáp án:
Áp dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)\).
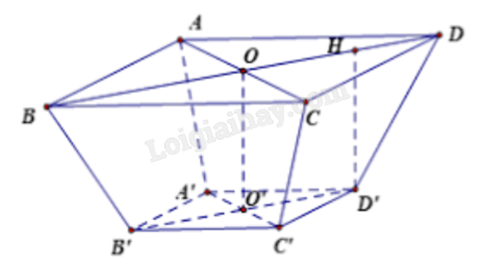
Đặt tên các điểm như hình vẽ, H là hình chiếu vuông góc của D’ lên mặt phẳng (ABCD).
Khi đó AB = 80, A’B’ = 60, DD’ = 50.
Áp dụng công thức tính đường chéo hình vuông, ta có \(BD = 80\sqrt 2 \), \(B'D' = 60\sqrt 2 \).
\(DH = \frac{{BD - B'D'}}{2} = \frac{{80\sqrt 2 - 60\sqrt 2 }}{2} = 10\sqrt 2 \).
Chiều cao sọt là \(h = D'H = \sqrt {D'{D^2} - D'{H^2}} = \sqrt {{{50}^2} - {{\left( {10\sqrt 2 } \right)}^2}} = 10\sqrt {23} \).
Thể tích sọt có dạng khối chóp cụt đều là:
$V=\frac{1}{3}h\left( {{S}_{1}}+\sqrt{{{S}_{1}}{{S}_{2}}}+{{S}_{2}} \right)=\frac{1}{3}10\sqrt{23}\left( {{80}^{2}}+\sqrt{{{80}^{2}}{{.60}^{2}}}+{{60}^{2}} \right)$
$\approx 236594$ $c{{m}^{3}}\approx 0,24$ ${{m}^{3}}$.
Để cái thang có thể tựa vào tường và mặt đất, ngang qua cột đỡ cao 4 m, song song và cách tường 0,5 m kể từ gốc của cột đỡ như hình vẽ thì chiều dài bé nhất của cái thang là \(\sqrt {\frac{a}{b}} \), biết \(\frac{a}{b}\) là phân số tối giản và \(a,b \in {\mathbb{N}^*}\). Khi đó a + 5b bằng bao nhiêu?
Đáp án:
Đáp án:
Lập hàm số biểu diễn chiều dài của thang theo biến x. Tìm giá trị nhỏ nhất của hàm số đó.
Đặt HC = x > 0. Suy ra BC = x + 0,5.
Áp dụng định lí Thales, ta có \(\frac{{HC}}{{BC}} = \frac{{MH}}{{AB}} \Leftrightarrow \frac{x}{{x + 0,5}} = \frac{4}{{AB}} \Leftrightarrow AB = \frac{{4(x + 0,5)}}{x}\).
Vì tam giác ABC vuông tại B nên suy ra \(A{C^2} = A{B^2} + B{C^2} = \frac{{16{{(x + 0,5)}^2}}}{{x}^2} + {(x + 0,5)^2} = f(x)\).
Để chiều dài thang nhỏ nhất thì AC nhỏ nhất, hay \(A{C^2}\) nhỏ nhất.
Bài toán trở thành tìm giá trị nhỏ nhất của f(x) với x > 0.
\(f'(x) = \frac{{\left( {4{x^3} + 3{x^2} + \frac{{65}}{2}x + 16} \right){x^2} - 2x\left( {{x^4} + {x^3} + \frac{{65}}{2}{x^2} + 16x + 4} \right)}}{{{x^4}}} = \frac{{2{x^4} + {x^3} - 16x - 8}}{{{x^3}}}\).
\(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - \frac{1}{2}\end{array} \right.\). Loại \(x = - \frac{1}{2} < 0\).
Ta có bảng biến thiên:
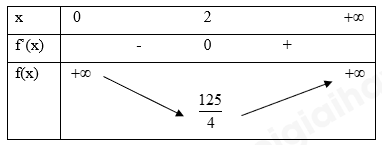
Vậy chiều dài thang nhỏ nhất là \(AC = \sqrt {\frac{{125}}{4}} \). Khi đó a + 5b = 125 + 5.4 = 145.
Một chiếc đèn trang trí (gồm các bóng đèn gắn vào một giá hình tròn) như hình bên dưới. Đèn được treo song song với mặt phẳng nằm ngang bởi ba sợi dây không dãn xuất phát từ điểm O trên trần nhà và lần lượt buộc vào ba điểm A, B, C trên giá sao cho tam giác ABC đều. Độ dài của ba đoạn dây OA, OB, OC đều bằng L, trọng lượng của chiếc đèn là 27 N, bán kính của giá hình tròn là 0,5 m.

Biết rằng mỗi sợi dây đó được thiết kế để chịu được lực căng tối đa là 12 N . Hỏi chiều dài tối thiểu của mỗi sợi dây là bao nhiêu mét (kết quả làm tròn đến hàng phần trăm)?
Đáp án:
Đáp án:
Áp dụng quy tắc tổng hợp lực, tính chất vecto của trọng tâm tam giác.
Gọi G là trọng tâm tam giác ABC. Vì tam giác ABC đều nên G là tâm đường tròn ngoại tiếp tam giác ABC . Do đó, GA = GB = GC = 0,5 m.
Theo đề bài, ta có OA = OB = OC = L nên \(OG \bot (ABC)\) và \(\left| {\overrightarrow {OA} } \right| = \left| {\overrightarrow {OB} } \right| = \left| {\overrightarrow {OC} } \right| = L\).
Gọi F là độ lớn của các lực căng \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \), \(\overrightarrow {{F_3}} \) trên mỗi sợi dây. Khi đó, F = F(L) là một hàm số với biến số L.
Ta có \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right| = F\) và tồn tại hằng số \(k \ne 0\) sao cho \(\overrightarrow {{F_1}} = k\overrightarrow {OA} \), \(\overrightarrow {{F_2}} = k\overrightarrow {OB} \), \(\overrightarrow {{F_3}} = k\overrightarrow {OC} \).
Suy ra \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = k\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right) = k.3\overrightarrow {OG} \).
Mặt khác, có \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P \) với \(\overrightarrow P \) là trọng lực tác dụng lên chiếc đèn.
Suy ra \(\left| {\overrightarrow P } \right| = 27 \Rightarrow k.3\left| {\overrightarrow {OG} } \right| = 27 \Leftrightarrow k = \frac{9}{{OG}}\).
Tam giác AOG vuông tại G nên \(OG = \sqrt {O{A^2} - G{A^2}} = \sqrt {{L^2} - 0,{5^2}} \) với L > 0,5.
Khi đó \(F(L) = \left| {\overrightarrow {{F_1}} } \right| = k\left| {\overrightarrow {OA} } \right| = \frac{{9L}}{{\sqrt {{L^2} - 0,{5^2}} }}\) (với L > 0,5).
Suy ra \(F(L) \le 12 \Leftrightarrow \frac{{9L}}{{\sqrt {{L^2} - 0,{5^2}} }} \le 12 \Leftrightarrow 3L \le 4\sqrt {{L^2} - 0,{5^2}} \)
\(\Leftrightarrow 9{L^2} \le 16{L^2} - 4 \Leftrightarrow 7{L^2} \ge 4 \Leftrightarrow L \ge \frac{{2\sqrt 7 }}{7}\).
Vậy chiều dài tối thiểu của mỗi sợi dây là \(\frac{{2\sqrt 7 }}{7} \approx 0,76\) (m).
Hai chiếc khinh khí cầu A và B bay lên từ cùng một vị trí O trên mặt đất. Sau một khoảng thời gian, khinh khí cầu A nằm cách điểm xuất phát 4 km về phía Đông và 3km về phía Nam, đồng thời cách mặt đất 1 km; khinh khí cầu B nằm cách điểm xuất phát 1 km về phía Bắc và 1,5 km về phía Tây, đồng thời cách mặt đất 0,8 km (hình minh họa bên dưới). Cùng thời điểm đó, một người đứng trên mặt đất và nhìn thấy hai khinh khí cầu nói trên. Biết rằng, so với các vị trí quan sát khác trên mặt đất, vị trí người đó đứng có tổng khoảng cách đến hai khinh khí cầu là nhỏ nhất. Hỏi tổng khoảng cách nhỏ nhất ấy bằng bao nhiêu kilômét (làm tròn kết quả đến hàng phần trăm)?

Đáp án:
Đáp án:
Gọi vị trí người quan sát là M, điểm B’ đối xứng với B qua mặt phẳng Oxy.
MA + MB ngắn nhất khi MA + MB’ ngắn nhất.
Chọn hệ trục tọa độ Oxyz sao cho điểm xuất phát là gốc O như hình vẽ trên.
Khi đó tọa độ hai khinh khí cầu là A(3;4;1) và \(B\left( { - 1; - \frac{3}{2};\frac{4}{5}} \right)\).
Gọi M là vị trí người quan sát và \(B'\left( { - 1; - \frac{3}{2}; - \frac{4}{5}} \right)\) là điểm đối xứng với B qua mặt phẳng (Oxy).
Khi đó \(MA + MB = MA + MB' \ge AB' = \sqrt {{{\left( {3 + 1} \right)}^2} + {{\left( {4 + \frac{3}{2}} \right)}^2} + {{\left( {1 + \frac{4}{5}} \right)}^2}} \approx 7,03\) km.
Dấu “=” xảy ra khi và chỉ khi M, A, B’ thẳng hàng và M thuộc đoạn AB’.
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
Đề KSCL Toán 12 lần 1 năm 2025 - 2026 trường THPT Triệu Sơn 3 - Thanh Hóa
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường THPT Cửa Lò - Nghệ An
Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2026 trường Lê Thánh Tông - TP HCM
Đề khảo sát chất lượng Toán 12 lần 1 năm 2024 - 2025 trường THPT Nguyễn Đăng Đạo - Bắc Ninh
Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
Các bài khác cùng chuyên mục
- Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
- Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
- Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Triệu Sơn 3 - Thanh Hóa
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường THPT Cửa Lò - Nghệ An
- Đề thi thử THPT môn Toán lần 1 năm 2026 liên trường THPT Nghệ An
- Đề thi thử THPT môn Toán năm 2026 Sở GD&ĐT Bắc Ninh
- Đề thi thử THPT môn Toán lần 1 năm 2026 cụm trường THPT Đà Nẵng
- Đề khảo sát chất lượng Toán 12 lần 1 năm 2025 - 2026 trường THPT Triệu Sơn 3 - Thanh Hóa
- Đề thi thử THPT môn Toán lần 1 năm 2026 trường THPT Cửa Lò - Nghệ An









Bình luận