-
Đề thi chính thức tốt nghiệp THPT môn Toán
-
Đề thi thử tốt nghiệp THPT môn Toán
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Vĩnh Phúc
- Đề thi thử tốt nghiệp THPT môn Toán năm 2025 Sở GD Hà Tĩnh
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Ninh Bình
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 3 - Thanh Hóa
- Đề thi thử tốt nghiệp THPT môn Toán lần 1 năm 2025 cụm các trường số 4 - Hải Dương
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 sở GD&ĐT Phú Thọ
- Đề KSCL Toán 12 lần 1 năm 2024 - 2025 trường THPT Triệu Sơn 4 - Thanh Hóa
- Đề thi thử tốt nghiệp THPT môn Toán năm 2025 Sở GD Quảng Bình
- Đề KSCL Toán 11 năm 2024 - 2025 sở GD&ĐT Hà Nội
- Đề KSCL Toán 12 năm 2024 - 2025 sở GD&ĐT Hà Nội
-
Đề tham khảo thi tốt nghiệp THPT môn Toán
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 1
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 2
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 3
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 4
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 5
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 6
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 7
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 8
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 9
- Đề tham khảo thi tốt nghiệp THPT môn Toán - Đề số 10
Đề thi THPT môn Toán năm 2025 (Mã 123) có lời giải
Đề thi tốt nghiệp THPT môn Toán năm 2025 - Mã 123
Đề bài
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng $(ABC)$, tam giác ABC vuông tại $A$ và $SA = 3$, $AB = 4$, $AC = 5$. Thể tích của khối chóp S.ABC bằng
-
A.
60.
-
B.
20.
-
C.
30.
-
D.
10.
Nghiệm của phương trình $\log_{3}(2x - 1) = 2$ là
-
A.
$x = \dfrac{5}{2}$.
-
B.
$x = 4$.
-
C.
$x = \dfrac{7}{2}$.
-
D.
$x = 5$.
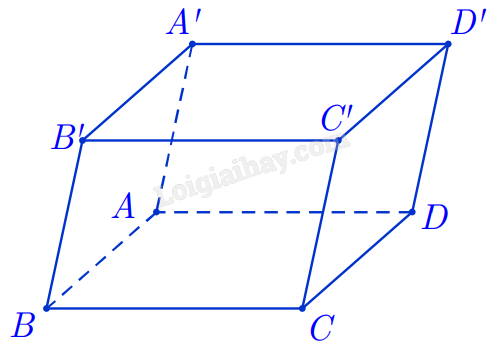
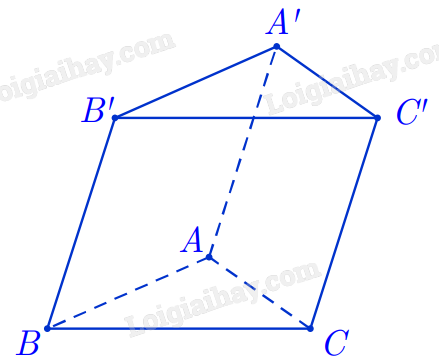
Cho hình hộp ABCD.A'B'C'D' (xem hình dưới). Đường thẳng AB song song với mặt phẳng nào sau đây?
-
A.
(CC'A'A).
-
B.
(BB'C'C).
-
C.
(A'B'C'D').
-
D.
(AA'DD).
Họ nguyên hàm của hàm số $f(x) = x^{2}$ là
-
A.
$\dfrac{1}{2}x^{3} + C$.
-
B.
$2x^{3} + C$.
-
C.
$3x^{2} + C$.
-
D.
$\dfrac{1}{3}x^{3} + C$.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $(d)$: $\dfrac{x - 3}{4} = \dfrac{y + 2}{- 5} = \dfrac{z - 1}{2}$. Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng $(d)$?
-
A.
$\overset{\rightarrow}{u_{1}} = (3; - 2;1)$.
-
B.
$\overset{\rightarrow}{u_{2}} = (4;5;2)$.
-
C.
$\overset{\rightarrow}{u_{3}} = (3;2;1)$.
-
D.
$\overset{\rightarrow}{u_{4}} = (4; - 5;2)$.
Cho cấp số cộng $(u_{n})$ có $u_{1} = 4$ và công sai $d = - 3$. Giá trị của $u_{5}$ bằng
-
A.
16.
-
B.
19.
-
C.
-11.
-
D.
-8.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm $A(2;1; - 4)$ nhận $\overset{\rightarrow}{u} = (3;2; - 1)$ làm một vectơ pháp tuyến có phương trình là
-
A.
$2(x - 3) + (y - 2) - 4(z + 1) = 0$.
-
B.
$3(x - 2) + 2(y - 1) - (z + 4) = 0$.
-
C.
$3(x + 2) + 2(y + 1) - (z - 4) = 0$.
-
D.
$2(x + 3) + (y + 2) - 4(z - 1) = 0$.
Tập nghiệm của phương trình $\sin x = 0$ là
-
A.
$S = \left\{ k2\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
B.
$S = \left\{ k\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
C.
$S = \left\{ \dfrac{\pi}{2} + k\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
D.
$S = \left\{ \dfrac{\pi}{2} + k2\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
A.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{C^{\prime}B^{\prime}}$.
-
B.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC}$.
-
C.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC^{\prime}}$.
-
D.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{A^{\prime}A}$.
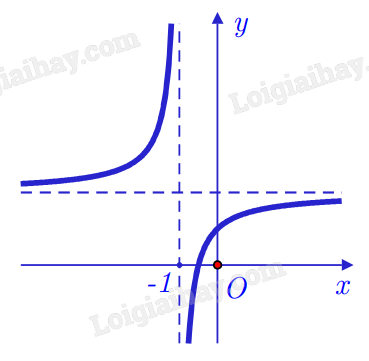
Cho hàm số $y = \dfrac{ax + b}{cx + d}$ ($ac \neq 0$, $ad - bc \neq 0$) có đồ thị như hình bên. Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
-
A.
$y = - 1$.
-
B.
$x = - 1$.
-
C.
$y = 2$.
-
D.
$x = 2$.
Trong mặt phẳng với hệ tọa độ Oxy, diện tích $S$ của hình phẳng giới hạn bởi đồ thị của hàm số $y = 2x - 3$, trục hoành và hai đường thẳng $x = 1$, $x = 2$ được xác định bằng công thức
-
A.
$S = \pi{\int_{1}^{2}{(2x - 3)}^{2}}dx$.
-
B.
$S = {\int_{1}^{2}{(2x - 3)}}dx$.
-
C.
$S = \pi{\int_{1}^{2}{(2x - 3)}^{2}}dx$.
-
D.
$\left. S = \left. \int_{1}^{2} \right|2x - 3 \middle| dx \right.$.
Một người chia thời lượng (đơn vị: giây) thực hiện các cuộc gọi điện thoại của mình trong một tuần thành sáu nhóm và lập bảng tần số ghép nhóm như sau.
Tứ phân vị thứ ba $Q_{3}$ (đơn vị: giây) của mẫu số liệu ghép nhóm trên bằng
-
A.
140.
-
B.
130.
-
C.
135.
-
D.
14.
Cho hàm số $f(x) = x^{3} - 48x - 8$.
Một phần mềm nhận dạng tin nhắn quảng cáo trên điện thoại bằng cách dựa theo từ khóa để đánh dấu một số tin nhắn được gửi đến. Qua một thời gian dài sử dụng, người ta thấy rằng trong số tất cả các tin nhắn gửi đến, có 10% số tin nhắn bị đánh dấu. Trong số các tin nhắn bị đánh dấu, có 10% số tin nhắn không phải là quảng cáo. Trong số các tin nhắn không bị đánh dấu, có 10% số tin nhắn là quảng cáo. Chọn ngẫu nhiên một tin nhắn được gửi đến điện thoại.
Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ tọa độ Oxyz có $\overset{\rightarrow}{i},\overset{\rightarrow}{j},\overset{\rightarrow}{k}$ lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm $A$ và $B$, trong đó điểm $A$ có tọa độ là $(4;4;0)$. Một vật (coi như là một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian $t$ (giây) theo công thức $v(t) = \beta t + 300$ (m/giây), trong đó $\beta$ là hằng số dương và $0 \leq t \leq 6$. Ở thời điểm ban đầu ($t = 0$), vật đi qua $A$ với tốc độ 300 m/giây và hướng tới $B$. Sau 2 giây kể từ thời điểm ban đầu, vật đi được quãng đường 608 m. Gọi $\overset{\rightarrow}{u} = (a;b;c)$ là vectơ cùng hướng với vectơ $\overset{\rightarrow}{AB}$. Biết rằng $\left| \overset{\rightarrow}{u} \middle| = 1 \right.$ và góc giữa vectơ $\overset{\rightarrow}{u}$ lần lượt với các vectơ $\overset{\rightarrow}{i},\overset{\rightarrow}{j},\overset{\rightarrow}{k}$ có số đo tương ứng bằng $60^{o},60^{o},45^{o}$.
Đối với ngành nuôi trồng thủy sản, việc kiểm soát lượng thuốc tồn dư trong nước là một nhiệm vụ quan trọng nhằm đáp ứng các tiêu chuẩn an toàn về môi trường. Khi nghiên cứu một loại thuốc trị bệnh trong nuôi trồng thủy sản, người ta sử dụng thuốc đó một lần và theo dõi nồng độ thuốc tồn dư trong nước kể từ lúc sử dụng thuốc. Kết quả cho thấy nồng độ thuốc $y(t)$ (đơn vị: mg/lít) tồn dư trong nước tại thời điểm $t$ ngày ($t \geq 0$) kể từ lúc sử dụng thuốc, thỏa mãn $y(t) > 0$ và $y'(t) = k.y(t)$ ($t \geq 0$), trong đó $k$ là hằng số khác không. Đo nồng độ thuốc tồn dư trong nước tại các thời điểm $t = 6$ (ngày); $t = 12$ (ngày) nhận được kết quả lần lượt là 2 mg/lít; 1 mg/lít. Cho biết $y(t) = e^{g(t)}$ ($t \geq 0$).
Có bốn ngăn (trong một giá để sách) được đánh số thứ tự 1, 2, 3, 4 và bảy quyển sách khác nhau. Bạn An xếp hết bảy quyển sách nói trên vào bốn ngăn đó sao cho mỗi ngăn có ít nhất một quyển sách và các quyển sách được xếp thẳng đứng thành một hàng ngang với gáy sách quay ra ngoài ở mỗi ngăn. Khi đã xếp xong bảy quyển sách, hai cách xếp của bạn An được gọi là giống nhau nếu chúng thỏa mãn đồng thời hai điều kiện sau đây:
+ Với từng ngăn, số lượng quyển sách ở ngăn đó là như nhau trong cả hai cách xếp;
+ Với từng ngăn, thứ tự từ trái sang phải của các quyển sách được xếp là như nhau trong cả hai cách xếp.
Gọi $T$ là số cách xếp đôi một khác nhau của bạn An. Giá trị của $\dfrac{T}{50}$ bằng bao nhiêu?
Để đặt được một vật trang trí trên mặt bàn, người ta thiết kế một chân để như sau. Lấy một khối gỗ có dạng khối chóp cụt tứ giác đều với độ dài hai cạnh đáy lần lượt bằng 7,4 cm và 10,4 cm, bề dày của khối gỗ bằng 1,5 cm. Sau đó khoét bỏ đi một phần của khối gỗ sao cho phần đó có dạng vật thể $(\mathcal{N})$, ở đó $(\mathcal{H})$ nhận được bằng cách cắt khối cầu bán kính 5,6 cm bởi một mặt phẳng cắt mà mặt cắt là hình tròn bán kính 3,5 cm (xem hình dưới).
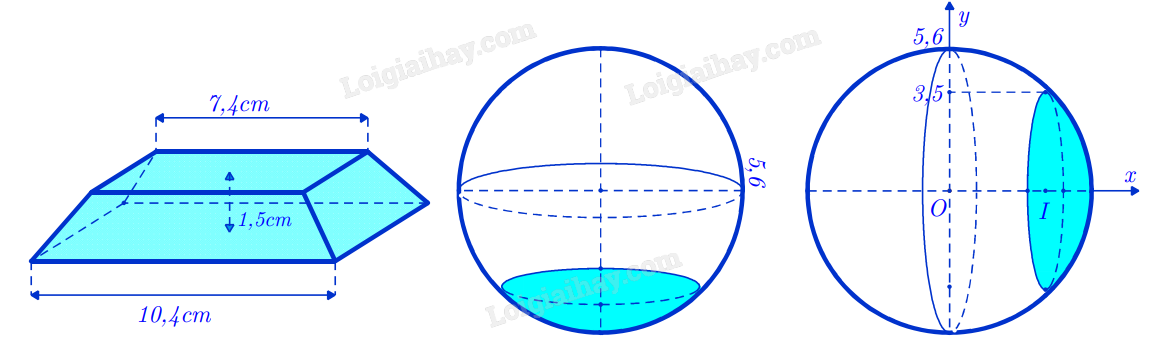
Thể tích của khối chân để bằng bao nhiêu centimet khối (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần mười)?
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với $\widehat{ABC} = 60^{o}$ và $AB = 4$. Biết rằng hình chiếu vuông góc của $S$ trên mặt phẳng $(ABCD)$ là trọng tâm $H$ của tam giác ABC và $SH = 2\sqrt{3}$. Khoảng cách giữa hai đường thẳng AC và SD bằng bao nhiêu (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần trăm)?
Để gây quỹ từ thiện, câu lạc bộ thiện nguyện của một trường THPT tổ chức hoạt động bán hàng với hai mặt hàng là nước chanh và khoai chiên. Câu lạc bộ thiết kế hai thực đơn. Thực đơn 1 có giá 25 nghìn đồng, bao gồm hai cốc nước chanh và một túi khoai chiên. Thực đơn 2 có giá 40 nghìn đồng, bao gồm ba cốc nước chanh và hai túi khoai chiên. Biết rằng câu lạc bộ chỉ làm được không quá 165 cốc nước chanh và 100 túi khoai chiên. Số tiền lớn nhất mà câu lạc bộ có thể nhận được sau khi bán hết hàng bằng bao nhiêu nghìn đồng?
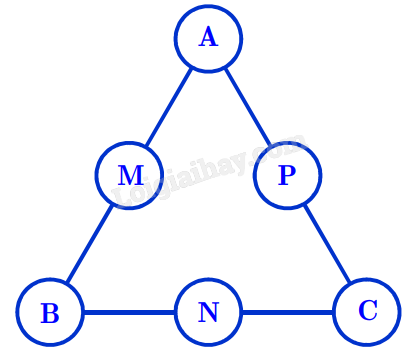
Bạn Nam tham gia cuộc thi giải một mật thư. Theo quy tắc của cuộc thi, người chơi cần chọn ra sáu số từ tập $S = \left\{ 31;32;33;34;35;36;37;38;39 \right\}$ và xếp mỗi số vào đúng một vị trí trong sáu vị trí A, B, C, M, N, P như hình bên sao cho mỗi vị trí chỉ được xếp một số. Mật thư sẽ được giải nếu các bộ ba số xuất hiện ở những bộ ba vị trí $(A,M,B)$; $(B,N,C)$; $(C,P,A)$ tạo thành các cấp số cộng theo thứ tự đó. Bạn Nam chọn ngẫu nhiên sáu số trong tập $S$ và xếp ngẫu nhiên vào các vị trí được yêu cầu. Gọi xác suất để bạn Nam giải được mật thư ở lần chọn và xếp đó là $\dfrac{a}{b}$. Giá trị của $\dfrac{b}{a}$ bằng bao nhiêu?
Nếu một doanh nghiệp sản xuất $x$ sản phẩm trong một tháng ($x \in {\mathbb{N}};1 \leq x \leq 4500$) thì doanh thu nhận được khi bán hết số sản phẩm đó là $F(x) = - 0,01x^{2} + 350x$ (nghìn đồng), trong khi chi phí sản xuất bình quân cho mỗi sản phẩm là $G(x) = \dfrac{30000}{x} + 260$ (nghìn đồng). Giả sử sản phẩm sản xuất ra luôn được bán hết. Trong một tháng, doanh nghiệp đó cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được lớn hơn 100 triệu đồng?
Lời giải và đáp án
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng $(ABC)$, tam giác ABC vuông tại $A$ và $SA = 3$, $AB = 4$, $AC = 5$. Thể tích của khối chóp S.ABC bằng
-
A.
60.
-
B.
20.
-
C.
30.
-
D.
10.
Đáp án : D
$V = \dfrac{1}{3}Sh$.
Thể tích khối chóp được tính bằng công thức:
$V = \dfrac{1}{3}.SA.S_{ABC} = \dfrac{1}{3}.3.\left( \dfrac{4.5}{2} \right) = 10$.
Nghiệm của phương trình $\log_{3}(2x - 1) = 2$ là
-
A.
$x = \dfrac{5}{2}$.
-
B.
$x = 4$.
-
C.
$x = \dfrac{7}{2}$.
-
D.
$x = 5$.
Đáp án : D
$\left. \log_{a}x = b\Leftrightarrow\left\{ \begin{array}{l} {x > 0} \\ {x = a^{b}} \end{array} \right. \right.$
$\log_{3}(2x - 1) = 2$
$\left. \Leftrightarrow 2x - 1 = 3^{2} \right.$
$\left. \Leftrightarrow 2x - 1 = 9 \right.$
$\left. \Leftrightarrow x = 5 \right.$.
Cho hình hộp ABCD.A'B'C'D' (xem hình dưới). Đường thẳng AB song song với mặt phẳng nào sau đây?
-
A.
(CC'A'A).
-
B.
(BB'C'C).
-
C.
(A'B'C'D').
-
D.
(AA'DD).
Đáp án : C
Đường thẳng song song với mặt phẳng nếu nó song song với một đường thẳng thuộc mặt phẳng đó.
Vì AB // A'B' nên AB // (A'B'C'D').
Họ nguyên hàm của hàm số $f(x) = x^{2}$ là
-
A.
$\dfrac{1}{2}x^{3} + C$.
-
B.
$2x^{3} + C$.
-
C.
$3x^{2} + C$.
-
D.
$\dfrac{1}{3}x^{3} + C$.
Đáp án : D
Áp dụng công thức nguyên hàm của hàm số lũy thừa.
${\int x^{2}}dx = \dfrac{1}{3}x^{3} + C$.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $(d)$: $\dfrac{x - 3}{4} = \dfrac{y + 2}{- 5} = \dfrac{z - 1}{2}$. Vectơ nào sau đây là một vectơ chỉ phương của đường thẳng $(d)$?
-
A.
$\overset{\rightarrow}{u_{1}} = (3; - 2;1)$.
-
B.
$\overset{\rightarrow}{u_{2}} = (4;5;2)$.
-
C.
$\overset{\rightarrow}{u_{3}} = (3;2;1)$.
-
D.
$\overset{\rightarrow}{u_{4}} = (4; - 5;2)$.
Đáp án : D
Đường thẳng $\dfrac{x - x_{0}}{a} = \dfrac{y - y_{0}}{b} = \dfrac{z - z_{0}}{c}$ có một vectơ chỉ phương là $\overset{\rightarrow}{u} = (a;b;c)$.
Vectơ chỉ phương của đường thẳng là $\overset{\rightarrow}{u_{4}} = (4; - 5;2)$.
Cho cấp số cộng $(u_{n})$ có $u_{1} = 4$ và công sai $d = - 3$. Giá trị của $u_{5}$ bằng
-
A.
16.
-
B.
19.
-
C.
-11.
-
D.
-8.
Đáp án : D
Áp dụng công thức số hạng tổng quát của cấp số cộng $u_{n} = u_{1} + (n - 1)d$.
$u_{5} = u_{1} + 4d = 4 + 4.( - 3) = - 8$.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm $A(2;1; - 4)$ nhận $\overset{\rightarrow}{u} = (3;2; - 1)$ làm một vectơ pháp tuyến có phương trình là
-
A.
$2(x - 3) + (y - 2) - 4(z + 1) = 0$.
-
B.
$3(x - 2) + 2(y - 1) - (z + 4) = 0$.
-
C.
$3(x + 2) + 2(y + 1) - (z - 4) = 0$.
-
D.
$2(x + 3) + (y + 2) - 4(z - 1) = 0$.
Đáp án : B
Mặt phẳng đi qua điểm $M\left( {x_{0};y_{0};z_{0}} \right)$, nhận $\overset{\rightarrow}{u} = (a;b;c)$ làm vectơ pháp tuyến có phương trình $a\left( {x - x_{0}} \right) + b\left( {y - y_{0}} \right) + c\left( {z - z_{0}} \right) = 0$.
Phương trình mặt phẳng: $3(x - 2) + 2(y - 1) - (z + 4) = 0$.
Tập nghiệm của phương trình $\sin x = 0$ là
-
A.
$S = \left\{ k2\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
B.
$S = \left\{ k\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
C.
$S = \left\{ \dfrac{\pi}{2} + k\pi \middle| k \in {\mathbb{Z}} \right\}$.
-
D.
$S = \left\{ \dfrac{\pi}{2} + k2\pi \middle| k \in {\mathbb{Z}} \right\}$.
Đáp án : B
Áp dụng công thức nghiệm của phương trình lượng giác cơ bản.
Nghiệm của phương trình $\sin x = 0$ là $x = k\pi$ $\left( {k \in {\mathbb{Z}}} \right)$.
-
A.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{C^{\prime}B^{\prime}}$.
-
B.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC}$.
-
C.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BC^{\prime}}$.
-
D.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{A^{\prime}A}$.
Đáp án : B
Áp dụng quy tắc ba điểm.
$\overset{\rightarrow}{BA} + \overset{\rightarrow}{A^{\prime}C^{\prime}} = \overset{\rightarrow}{BA} + \overset{\rightarrow}{AC} = \overset{\rightarrow}{BC}$.
Cho hàm số $y = \dfrac{ax + b}{cx + d}$ ($ac \neq 0$, $ad - bc \neq 0$) có đồ thị như hình bên. Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
-
A.
$y = - 1$.
-
B.
$x = - 1$.
-
C.
$y = 2$.
-
D.
$x = 2$.
Đáp án : B
Quan sát đồ thị và nhận xét.
Tiệm cận đứng của đồ thị hàm số là $x = - 1$.
Trong mặt phẳng với hệ tọa độ Oxy, diện tích $S$ của hình phẳng giới hạn bởi đồ thị của hàm số $y = 2x - 3$, trục hoành và hai đường thẳng $x = 1$, $x = 2$ được xác định bằng công thức
-
A.
$S = \pi{\int_{1}^{2}{(2x - 3)}^{2}}dx$.
-
B.
$S = {\int_{1}^{2}{(2x - 3)}}dx$.
-
C.
$S = \pi{\int_{1}^{2}{(2x - 3)}^{2}}dx$.
-
D.
$\left. S = \left. \int_{1}^{2} \right|2x - 3 \middle| dx \right.$.
Đáp án : D
Áp dụng công thức tính diện tích hình phẳng $S = {\int\limits_{a}^{b}{\left| {f(x)} \right|dx}}$.
Diện tích hình phẳng: $S = {\int_{1}^{2}{\left| {2x - 3} \right|dx}}$.
Một người chia thời lượng (đơn vị: giây) thực hiện các cuộc gọi điện thoại của mình trong một tuần thành sáu nhóm và lập bảng tần số ghép nhóm như sau.
Tứ phân vị thứ ba $Q_{3}$ (đơn vị: giây) của mẫu số liệu ghép nhóm trên bằng
-
A.
140.
-
B.
130.
-
C.
135.
-
D.
14.
Đáp án : C
Áp dụng công thức tính $Q_{3}$ của mẫu số liệu ghép nhóm.
$\left. n = 40\Rightarrow\dfrac{3n}{4} = 30\Rightarrow Q_{3} \right.$ thuộc nhóm [120;160).
$Q_{3} = 120 + \dfrac{\dfrac{3.40}{4} - (11 + 10 + 6)}{8}(160 - 120) = 135$.
Cho hàm số $f(x) = x^{3} - 48x - 8$.
Tính đạo hàm f’(x), tìm nghiệm của f’(x) = 0 và tìm giá trị lớn nhất của hàm số.
a) Đúng. $f'(x) = 3x^{2} - 48$.
b) Sai. Phương trình $f'(x) = 0$ có hai nghiệm $x = \pm 4$.
c) Sai. $f(4) = 4^{3} - 48.4 - 8 = - 136$.
d) Sai. Ta có:
f(4) = -136; f(-4) = 120; f(5) = 107; f(-5) = 123.
Do đó giá trị lớn nhất của f(x) trên [-5;5] là 120 (tại x = -4).
Một phần mềm nhận dạng tin nhắn quảng cáo trên điện thoại bằng cách dựa theo từ khóa để đánh dấu một số tin nhắn được gửi đến. Qua một thời gian dài sử dụng, người ta thấy rằng trong số tất cả các tin nhắn gửi đến, có 10% số tin nhắn bị đánh dấu. Trong số các tin nhắn bị đánh dấu, có 10% số tin nhắn không phải là quảng cáo. Trong số các tin nhắn không bị đánh dấu, có 10% số tin nhắn là quảng cáo. Chọn ngẫu nhiên một tin nhắn được gửi đến điện thoại.
Áp dụng công thức tính xác suất toàn phần, công thức Bayes.
Gọi A là biến cố “Tin nhắn bị đánh dấu”, suy ra $\overline{A}$ là biến cố “Tin nhắn không bị đánh dấu”.
B là biến cố “Tin nhắn là quảng cáo”, suy ra $\overline{B}$ là biến cố “Tin nhắn không phải quảng cáo”.
Theo giả thiết: P(A) = 0,1; $P\left( \overline{B} \middle| A \right) = 0.1$; $P\left( B \middle| \overline{A} \right) = 0.1$.
a) Đúng. Xác suất không bị đánh dấu:
$P(\overline{A}) = 1 - P(A) = 1 - 0,1 = 0,9$.
b) Sai. Xác suất không phải quảng cáo khi không bị đánh dấu:
$\left. P(\overline{B} \middle| \overline{A}) = 1 - P(B \middle| \overline{A}) = 1 - 0,1 = 0,9 \right.$.
c) Đúng. Xác suất không phải quảng cáo:
$\left. P(\overline{B}) = P(A).P(\overline{B} \middle| A) + P(\overline{A}).P(\overline{B} \middle| \overline{A}) = 0,1.0,1 + 0,9.0,9 = 0.82 \right.$.
d) Đúng. Xác suất không bị đánh dấu khi không phải quảng cáo:
$\left. P(\overline{A} \middle| \overline{B}) = \dfrac{\left. P(\overline{A}).P(\overline{B} \middle| \overline{A}) \right.}{P(\overline{B})} = \dfrac{0,9.0,9}{0,82} \approx 0,988 > 0,95 \right.$.
Mô hình toán học sau đây được sử dụng trong quan sát chuyển động của một vật. Trong không gian cho hệ tọa độ Oxyz có $\overset{\rightarrow}{i},\overset{\rightarrow}{j},\overset{\rightarrow}{k}$ lần lượt là các vectơ đơn vị trên các trục Ox, Oy, Oz và độ dài của mỗi vectơ đơn vị đó bằng 1 mét. Cho hai điểm $A$ và $B$, trong đó điểm $A$ có tọa độ là $(4;4;0)$. Một vật (coi như là một hạt) chuyển động thẳng với tốc độ phụ thuộc thời gian $t$ (giây) theo công thức $v(t) = \beta t + 300$ (m/giây), trong đó $\beta$ là hằng số dương và $0 \leq t \leq 6$. Ở thời điểm ban đầu ($t = 0$), vật đi qua $A$ với tốc độ 300 m/giây và hướng tới $B$. Sau 2 giây kể từ thời điểm ban đầu, vật đi được quãng đường 608 m. Gọi $\overset{\rightarrow}{u} = (a;b;c)$ là vectơ cùng hướng với vectơ $\overset{\rightarrow}{AB}$. Biết rằng $\left| \overset{\rightarrow}{u} \middle| = 1 \right.$ và góc giữa vectơ $\overset{\rightarrow}{u}$ lần lượt với các vectơ $\overset{\rightarrow}{i},\overset{\rightarrow}{j},\overset{\rightarrow}{k}$ có số đo tương ứng bằng $60^{o},60^{o},45^{o}$.
Áp dụng biểu thức tọa độ các phép toán vectơ.
a) Đúng. $\overset{\rightarrow}{u} = (a;b;c)$, $\left| \overset{\rightarrow}{u} \right| = 1$, $\overset{\rightarrow}{i} \in (1;0;1)$.
$\left. \cos(\overset{\rightarrow}{u},\overset{\rightarrow}{i}) = \dfrac{\overset{\rightarrow}{u} \cdot \overset{\rightarrow}{i}}{\left| \overset{\rightarrow}{u} \right|.\left| \overset{\rightarrow}{i} \right|} = \dfrac{a}{1.1} = a\Rightarrow a = \cos 60^{o} \right.$.
b) Sai. $a = \cos 60^{o} = \dfrac{1}{2}$.
Tương tự ta có $\left. b = \cos 60^{o} = \dfrac{1}{2};c = \cos 45^{o} = \dfrac{\sqrt{2}}{2}\Rightarrow\overset{\rightarrow}{u}\left( {\dfrac{1}{2},\dfrac{1}{2},\dfrac{\sqrt{2}}{2}} \right) \right.$.
$\left. \Rightarrow AB:\dfrac{x - 4}{1} = \dfrac{y - 4}{1} = \dfrac{z}{\sqrt{2}} \right.$.
c) Sai. $v(t) = \beta t + 300$, sau 2 giây, hạt đi được quãng đường là:
$\left. S = {\int_{0}^{2}{(\beta t + 300)}}dt = 608\Rightarrow 2\beta + 600 = 608\Rightarrow\beta = 4\text{~(Sai)} \right.$
d) Đúng. Sau 5 giây, hạt đi được quãng đường là:
$AB = {\int_{0}^{5}{(4t + 300)dt}} = 1550$.
$\left. \overset{\rightarrow}{AB} = k\overset{\rightarrow}{u}\Rightarrow\overset{\rightarrow}{AB} = k.\left| \overset{\rightarrow}{u} \right| = k.\sqrt{\dfrac{1}{4} + \dfrac{1}{4} + \dfrac{1}{2}} = k\Rightarrow k = 1550 \right.$.
$\left. \Rightarrow\overset{\rightarrow}{AB} = \left( {\dfrac{1500}{2};\dfrac{1500}{2};\dfrac{1500}{\sqrt{2}}} \right) \right.$.
$\left. \Rightarrow x_{B} = \dfrac{1500}{2} + x_{A} = \dfrac{1500}{2} + 4 = 779 \right.$.
Đối với ngành nuôi trồng thủy sản, việc kiểm soát lượng thuốc tồn dư trong nước là một nhiệm vụ quan trọng nhằm đáp ứng các tiêu chuẩn an toàn về môi trường. Khi nghiên cứu một loại thuốc trị bệnh trong nuôi trồng thủy sản, người ta sử dụng thuốc đó một lần và theo dõi nồng độ thuốc tồn dư trong nước kể từ lúc sử dụng thuốc. Kết quả cho thấy nồng độ thuốc $y(t)$ (đơn vị: mg/lít) tồn dư trong nước tại thời điểm $t$ ngày ($t \geq 0$) kể từ lúc sử dụng thuốc, thỏa mãn $y(t) > 0$ và $y'(t) = k.y(t)$ ($t \geq 0$), trong đó $k$ là hằng số khác không. Đo nồng độ thuốc tồn dư trong nước tại các thời điểm $t = 6$ (ngày); $t = 12$ (ngày) nhận được kết quả lần lượt là 2 mg/lít; 1 mg/lít. Cho biết $y(t) = e^{g(t)}$ ($t \geq 0$).
Thay số từ giả thiết vào hàm số để giải.
a) Đúng. $\left. y(t) = e^{g(t)}\Rightarrow y'(t) = e^{g(t)}.g'(t) \right.$.
$\left. y'(t) = k.y(t)\Leftrightarrow e^{g(t)}.g'(t) = k.e^{g(t)}\Rightarrow g'(t) = k\Rightarrow g(t) = kt + C \right.$.
b) Sai. $\left. t = 6\Rightarrow y(6) = 2\Leftrightarrow e^{6k + C} = 2\Leftrightarrow 6k + C = \ln 2 \right.$.
$\left. t = 12\Rightarrow y(12) = 1\Leftrightarrow e^{12k + C} = 1\Leftrightarrow 12k + C = 0 \right.$.
Suy ra $k = \dfrac{- 1}{6}\ln 2$.
c) Sai. $C = - 12k = 2\ln 2$.
d) Đúng. $\left. t = 28\Rightarrow y(28) = 1\Leftrightarrow e^{28{({\dfrac{1}{6}\ln 1})} + 2\ln 2} = 0,1575 < 0,2 \right.$.
Có bốn ngăn (trong một giá để sách) được đánh số thứ tự 1, 2, 3, 4 và bảy quyển sách khác nhau. Bạn An xếp hết bảy quyển sách nói trên vào bốn ngăn đó sao cho mỗi ngăn có ít nhất một quyển sách và các quyển sách được xếp thẳng đứng thành một hàng ngang với gáy sách quay ra ngoài ở mỗi ngăn. Khi đã xếp xong bảy quyển sách, hai cách xếp của bạn An được gọi là giống nhau nếu chúng thỏa mãn đồng thời hai điều kiện sau đây:
+ Với từng ngăn, số lượng quyển sách ở ngăn đó là như nhau trong cả hai cách xếp;
+ Với từng ngăn, thứ tự từ trái sang phải của các quyển sách được xếp là như nhau trong cả hai cách xếp.
Gọi $T$ là số cách xếp đôi một khác nhau của bạn An. Giá trị của $\dfrac{T}{50}$ bằng bao nhiêu?
Sử dụng phương pháp vách ngăn.
Ta có $7 = 1 + 1 + 1 + 4 = 1 = 1 + 2 + 3 = 1 + 2 + 2 + 2$.
TH1: Có 3 ngăn chứa 1 quyển sách, một ngăn chứa 4 quyển sách
Số cách xếp là $4.A_{7}^{4}.31 = 20160$.
TH2: Có hai ngăn chứa một quyển sách, một ngăn chứa 2 quyển sách, một ngăn chứa 3 quyển sách
Số cách xếp là $4.A_{7}^{3}.3A_{4}^{2}.21 = 60480$.
TH3: Có một ngăn chứa 1 quyển sách, ba ngăn còn lại mỗi ngăn chứa hai quyển sách
Số cách xếp là $4.A_{7}^{1}.A_{6}^{2}.A_{4}^{2}.A_{2}^{2} = 20160$.
$\left. T = 20160 = 60480 + 20160 = 100800\Rightarrow\dfrac{T}{50} = 2016 \right.$.
Để đặt được một vật trang trí trên mặt bàn, người ta thiết kế một chân để như sau. Lấy một khối gỗ có dạng khối chóp cụt tứ giác đều với độ dài hai cạnh đáy lần lượt bằng 7,4 cm và 10,4 cm, bề dày của khối gỗ bằng 1,5 cm. Sau đó khoét bỏ đi một phần của khối gỗ sao cho phần đó có dạng vật thể $(\mathcal{N})$, ở đó $(\mathcal{H})$ nhận được bằng cách cắt khối cầu bán kính 5,6 cm bởi một mặt phẳng cắt mà mặt cắt là hình tròn bán kính 3,5 cm (xem hình dưới).
Thể tích của khối chân để bằng bao nhiêu centimet khối (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần mười)?
Tính thể tích khối chóp cụt $V_{1}$ bằng cách áp dụng công thức $V = \dfrac{1}{3}h\left( {S + \sqrt{S.S'} + S'} \right)$.
Tính thể tích chỏm cầu $V_{2}$ bằng cách áp dụng công thức thể tích khối tròn xoay $V = \pi{\int\limits_{a}^{b}{f^{2}(x)dx}}$.
Thể tích chân đế là $V = V_{1} - V_{2}$.
Thể tích khối chóp cụt: $V_{1} = \dfrac{1}{3} \cdot 1,5 \cdot \left( {10,4^{2} + 7,4^{2} + 10,4 \cdot 7,4} \right)$.
Chỏm cầu sinh bởi hình phẳng giới hạn bởi đường tròn $x^{2} + y^{2} = 5,6^{2}$; Ox; $x = x_{I}$, $x = 5,6$.
$\left. OI = \sqrt{5,6^{2} - 3,5^{2}} = \dfrac{7\sqrt{39}}{10}\Rightarrow x_{I} = \dfrac{7\sqrt{39}}{10} \right.$.
Thể tích phần chỏm cầu: $\left. V_{2} = \pi{\int_{0}^{5,6}{\left( {5,6^{2} - x^{2}} \right)dx}}\Rightarrow x_{I} = \dfrac{7\sqrt{39}}{10} \right.$.
Thể tích chân đế: $V = V_{1} - V_{2} = 95,3$.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi với $\widehat{ABC} = 60^{o}$ và $AB = 4$. Biết rằng hình chiếu vuông góc của $S$ trên mặt phẳng $(ABCD)$ là trọng tâm $H$ của tam giác ABC và $SH = 2\sqrt{3}$. Khoảng cách giữa hai đường thẳng AC và SD bằng bao nhiêu (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần trăm)?
Xác định và tính độ dài đoạn vuông góc chung.
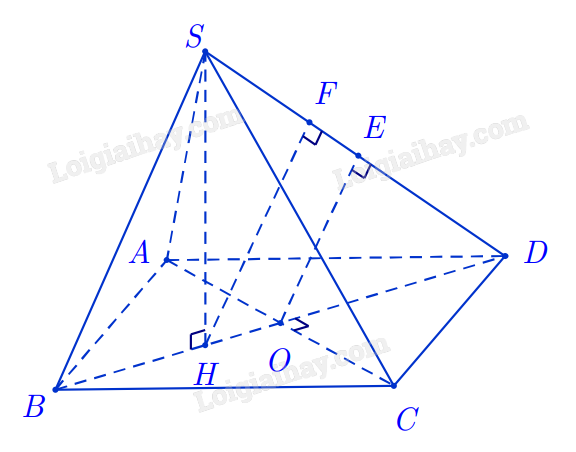
Ta có $AC\bot SH$ và $\left. BD\Rightarrow AC\bot(SBD) \right.$.
Kẻ OE, HF vuông góc với SD tại $E$ và $F$. Ta có OE là đoạn vuông góc chung của AC và SD.
Suy ra $d(AC,SD) = OE$.
Lại có $\dfrac{CE}{HF} = \dfrac{OD}{HD} = \dfrac{3}{4}$.
$HD = \dfrac{4}{3}OD = \dfrac{4}{3} \cdot 4 \cdot \dfrac{\sqrt{3}}{2} = \dfrac{8}{\sqrt{3}}$
$\left. \dfrac{1}{HF^{2}} = \dfrac{1}{HS^{2}} + \dfrac{1}{HD^{2}} = \dfrac{1}{12} + \dfrac{3}{64} = \dfrac{25}{192}\Rightarrow HF = \dfrac{\sqrt{192}}{25}\Rightarrow OE = \dfrac{3}{4} \cdot \dfrac{\sqrt{192}}{25} \approx 2,08 \right.$.
Để gây quỹ từ thiện, câu lạc bộ thiện nguyện của một trường THPT tổ chức hoạt động bán hàng với hai mặt hàng là nước chanh và khoai chiên. Câu lạc bộ thiết kế hai thực đơn. Thực đơn 1 có giá 25 nghìn đồng, bao gồm hai cốc nước chanh và một túi khoai chiên. Thực đơn 2 có giá 40 nghìn đồng, bao gồm ba cốc nước chanh và hai túi khoai chiên. Biết rằng câu lạc bộ chỉ làm được không quá 165 cốc nước chanh và 100 túi khoai chiên. Số tiền lớn nhất mà câu lạc bộ có thể nhận được sau khi bán hết hàng bằng bao nhiêu nghìn đồng?
Ứng dụng hệ bất phương trình bậc nhất hai ẩn.
Gọi số thực đơn 1 là $x$, số thực đơn 2 là $y$, ta có $x \geq 0$; $y \geq 0$.
Số cốc nước chanh là $2x + 3y \leq 165$.
Số túi khoai tây chiên là $x + 2y \leq 100$.
Số tiền thu về là $T = 25x + 40y$.
Xét hệ bất phương trình bậc nhất một ẩn:
$\left\{ \begin{array}{l} {x \geq 0} \\ {y \geq 0} \\ {2x + 3y \leq 165} \\ {x + 2y \leq 100} \end{array} \right.$
Miền nghiệm là tứ giác OABC với O(0;0), A(0;50), B(30;35), C(82,5;0).
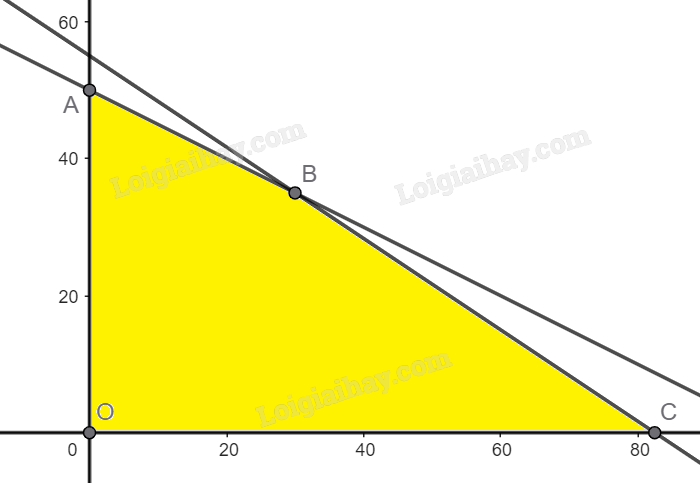
Ta có: $T_{O} = 25.0 + 40.0 = 0$;
$T_{A} = 25.0 + 40.50 = 200$;
$T_{B} = 25.30 + 40.35 = 2150$;
$T_{C} = 25.82,5 + 40.0 = 2062,5$.
Vậy số tiền lớn nhất câu lạc bộ nhận được khi bán hết hàng bằng 2150 nghìn đồng.
Bạn Nam tham gia cuộc thi giải một mật thư. Theo quy tắc của cuộc thi, người chơi cần chọn ra sáu số từ tập $S = \left\{ 31;32;33;34;35;36;37;38;39 \right\}$ và xếp mỗi số vào đúng một vị trí trong sáu vị trí A, B, C, M, N, P như hình bên sao cho mỗi vị trí chỉ được xếp một số. Mật thư sẽ được giải nếu các bộ ba số xuất hiện ở những bộ ba vị trí $(A,M,B)$; $(B,N,C)$; $(C,P,A)$ tạo thành các cấp số cộng theo thứ tự đó. Bạn Nam chọn ngẫu nhiên sáu số trong tập $S$ và xếp ngẫu nhiên vào các vị trí được yêu cầu. Gọi xác suất để bạn Nam giải được mật thư ở lần chọn và xếp đó là $\dfrac{a}{b}$. Giá trị của $\dfrac{b}{a}$ bằng bao nhiêu?
Chia trường hợp, sử dụng phương pháp tổ hợp.
Số phần tử của không gian mẫu là $n(\Omega) = A_{9}^{6} = 60480$.
Mật khẩu mở được khi $\left\{ \begin{array}{l} {A + B = 2M} \\ {B + C = 2N} \\ {C + A = 2P} \end{array} \right.$, suy ra A, B, C có cùng tính chẵn lẻ.
TH1: $A,B,C \in \left\{ 32;34;36;38 \right\}$.
- Chọn {A; B; C} đảm bảo không phải là 3 số chẵn liên tiếp, có 2 cách là $\left\{ 32;34;38 \right\},\left\{ 32;36;38 \right\}$.
- Xếp A, B, C có 3! = 6 cách.
- Xếp M, N, P có 1 cách.
Suy ra TH1 có 2.6 = 12 cách.
TH2: $A,B,C \in \left\{ 31;33;35;37;39 \right\}$.
- Chọn {A; B; C} đảm bảo không phải là 3 số lẻ cách đều nhau, có $C_{5}^{3} - 4 = 6$ cách (các cách loại là $\left\{ 31;33;35 \right\},\left\{ 33;35;37 \right\},\left\{ 35;37;39 \right\},\left\{ 31;35;39 \right\}$).
- Xếp A, B, C có 3! = 6 cách.
- Xếp M, N, P có 1 cách.
Suy ra TH2 có 6.6 = 36 cách.
Xác suất để mật khẩu mở được là: $\left. a = \dfrac{12 + 48}{60480}\Rightarrow\dfrac{3}{a} = 3780 \right.$.
Nếu một doanh nghiệp sản xuất $x$ sản phẩm trong một tháng ($x \in {\mathbb{N}};1 \leq x \leq 4500$) thì doanh thu nhận được khi bán hết số sản phẩm đó là $F(x) = - 0,01x^{2} + 350x$ (nghìn đồng), trong khi chi phí sản xuất bình quân cho mỗi sản phẩm là $G(x) = \dfrac{30000}{x} + 260$ (nghìn đồng). Giả sử sản phẩm sản xuất ra luôn được bán hết. Trong một tháng, doanh nghiệp đó cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được lớn hơn 100 triệu đồng?
Ứng dụng giải bất phương trình bậc hai một ẩn để giải bài toán.
Doanh thu $F(x) = - 0,01x^{2} + 350x$.
Chi phí $xG(x) = 30000 + 260x$.
Lợi nhuận $L(x) = F(x) - xG(x) = - 0,01x^{2} + 90x - 30000$.
Điều kiện $\left. - 0,01x^{2} + 90x - 30000 > 100000\Leftrightarrow 1807,42 < x < 7192,58 \right.$.
Các bài khác cùng chuyên mục
