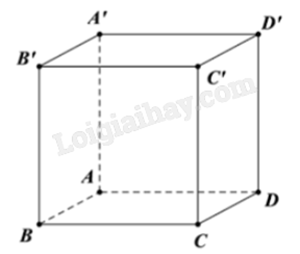
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa mặt phẳng (BDD’B’) và (ACC’A’) bằng
-
A.
\({45^o}\)
-
B.
\({60^o}\)
-
C.
\({30^o}\)
-
D.
\({90^o}\)
Đưa về tính góc giữa hai đường thẳng.
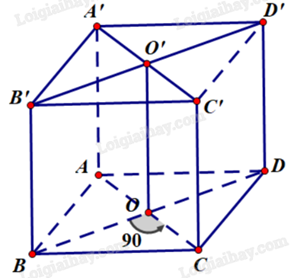
Gọi O là giao điểm của AC và BD, O’ là giao điểm của A’C’ và B’D’.
Ta có OO’ là giao tuyến của hai mặt phẳng (BDD’B’) và (ACC’A’) vì O, O’ cùng thuộc cả hai mặt phẳng trên.
Vì ABCD.A’B’C’D’ là hình lập phương nên dễ dàng chứng minh \(OO' \bot (ABCD) \Rightarrow \left\{ \begin{array}{l}OO' \bot BO\\OO' \bot CO\end{array} \right.\).
Ta có: \(\left\{ \begin{array}{l}BO \subset (BDD'B')\\CO \subset (ACC'A')\\BO \bot OO'\\CO \bot OO'\\OO' \subset (BDD'B') \cap (ACC'A')\end{array} \right.\) suy ra góc giữa hai mặt phẳng (BDD’B’) và (ACC’A’) là góc giữa hai đường thẳng BO và CO, hay BD và AC.
Vì ABCD là hình vuông nên \(AC \bot BD\).
Vậy góc giữa hai mặt phẳng (BDD’B’) và (ACC’A’) bằng \({90^o}\).
Đáp án : D

Các bài tập cùng chuyên đề
Góc giữa hai mặt phẳng bằng 00 khi nào, khác 00 khi nào?
Cho mặt phẳng (P) chứa đường thẳng b vuông góc với mặt phẳng (Q). Lấy một đường thẳng a vuông góc với (P) (H.7.47).
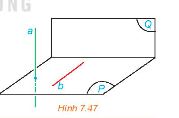
a) Tính góc giữa a và b.
b) Tính góc giữa (P) và (Q).
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong Hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế.
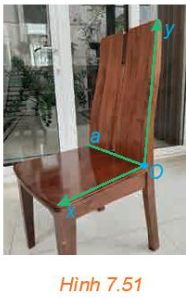
a) Theo tài liệu nói trên, góc nào trong hình nên có số đo từ 100° đến 105°?
b) Nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ bao nhiêu đến bao nhiêu độ?
Hai mái nhà trong Hình 7.72 là hai hình chữ nhật. Giả sử AB = 4,8m; OA = 2,8 m; OB = 4m.

a) Tính (gần đúng) số đo của góc nhị diện tạo bởi hai nửa mặt phẳng tương ứng chứa hai mái nhà.
b) Chứng minh rằng mặt phẳng (OAB) vuông góc với mặt đất phẳng.
Lưu ý: Đường giao giữa hai mái (đường nóc) song song với mặt đất.
c) Điểm A ở độ cao (so với mặt đất) hơn điểm B là 0,5 m. Tính (gần đúng) góc giữa mái nhà (chứa OB) so với mặt đất.
Độ dốc của mái nhà, mặt sân, con đường thẳng là tang của góc tạo bởi mái nhà mặt sân, con đường thẳng đó với mặt phẳng nằm ngang. Độ dốc của đường thẳng dành cho người khuyết tật được quy định là không quá \(\frac{1}{{12}}\). Hỏi theo đó, góc tạo bởi đường dành cho người khuyết tật và mặt phẳng nằm ngang không vượt quá bao nhiêu độ? (Làm tròn kết quả đến chữ số thập phân thứ hai).
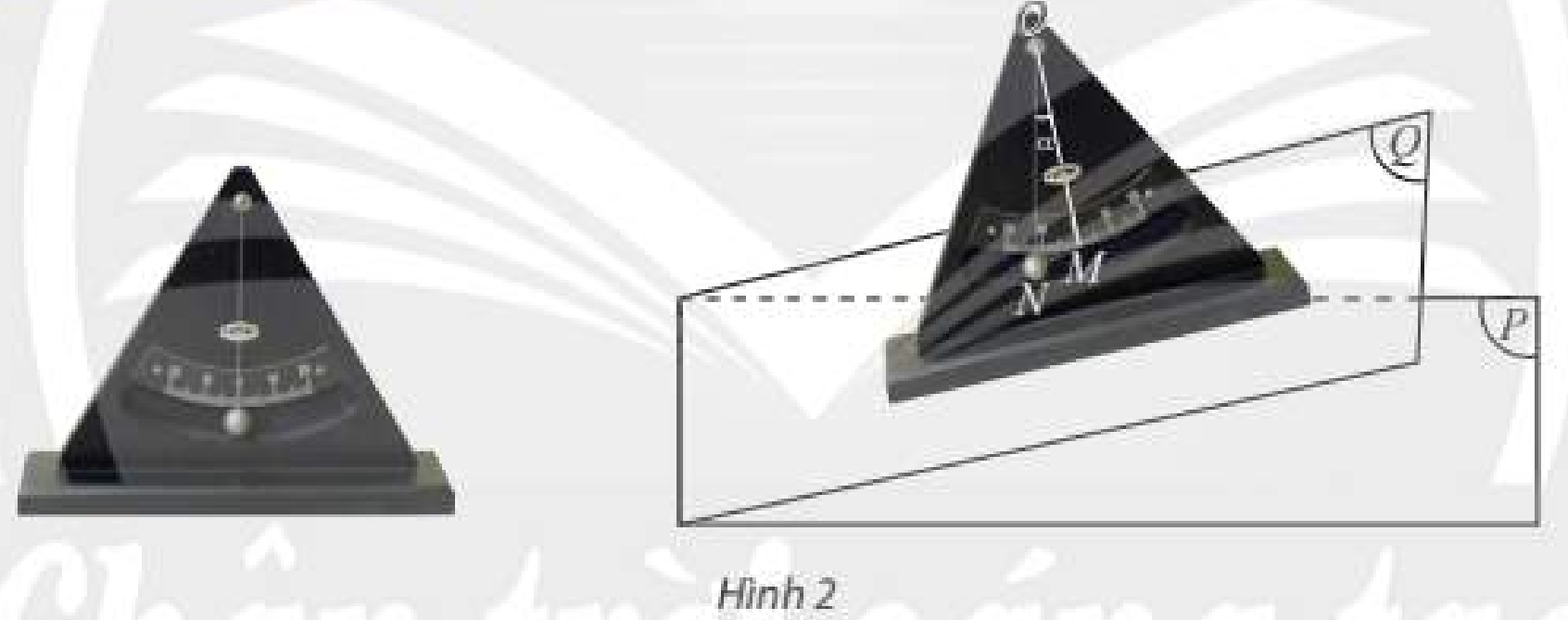
a) Có thể xác định góc giữa hai cánh của nắp hầm (Hình 1) bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh hay không?

b) Thế nào là góc giữa hai mặt phẳng? Tại sao thiết bị trong Hình 2 lại có thể đo được góc giữa mặt phẳng nghiêng \(\left( Q \right)\) và mặt đất \(\left( P \right)\).
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\) điểm \(M\) không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(H\) và \(K\) lần lượt là hình chiếu vuông góc của \(M\) lên \(\left( P \right)\) và \(\left( Q \right)\). Gọi \(O\) là giao điểm của \(d\) và \(\left( {MHK} \right)\) (Hình 8).
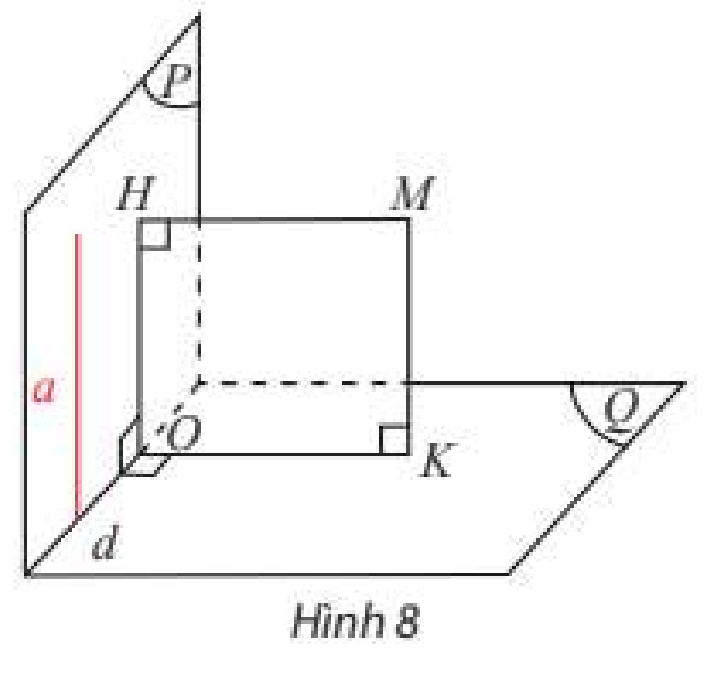
a) Giả sử \(\left( P \right) \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tìm trong \(\left( P \right)\) đường thẳng vuông góc với \(\left( Q \right)\).
b) Giả sử \(\left( P \right)\) chứa đường thẳng \(a\) với \(a \bot \left( Q \right)\), hãy cho biết tứ giác \(MHOK\) là hình gì? Tính góc giữa \(\left( P \right)\) và \(\left( Q \right)\).
Từ một điểm \(O\) vẽ hai tia \(Ox\) và \(Oy\) lần lượt vuông góc với hai bức tường trong phòng. Đo góc \(xOy\).
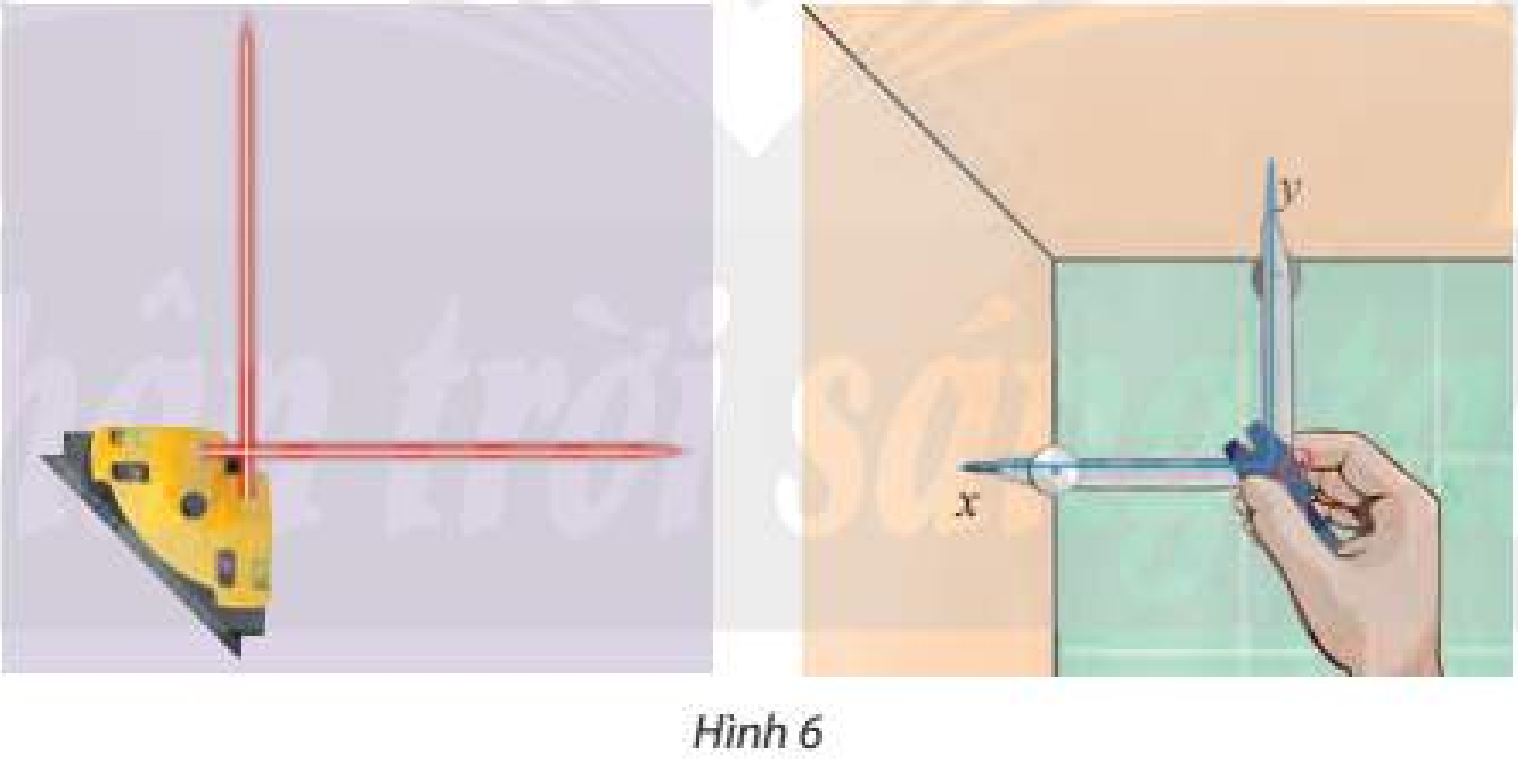
Cho góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\). Gọi \(O\) là một điểm tuỳ ý trên \(d\). \(Ox\) là tia nằm trong \(\left( P \right)\) và vuông góc với \(d\), \(Oy\) là tia nằm trong \(\left( Q \right)\) và vuông góc với \(d\) (Hình 6).
a) Nêu nhận xét về vị trí tương đối giữa \(d\) và \(mp\left( {Ox,Oy} \right)\).
b) Nêu nhận xét về số đo của góc \(xOy\) khi \(O\) thay đổi trên \(d\).

Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) cắt nhau theo giao tuyến \(d\). Hãy gọi tên các nửa mặt phẳng có chung bờ \(d\). Các nửa mặt phẳng này chia không gian thành bao nhiêu phần?
Cho tứ diện đều \(ABCD\) có độ dài các cạnh bằng \(a\). Gọi \(M\) là trung điểm của \(CD\), kẻ \(AH\) vuông góc với \(BM\) tại \(H\).
a) Chứng minh rằng \(AH \bot \left( {BCD} \right)\).
b) Tính côsin của góc giữa mặt phẳng \(\left( {BCD} \right)\) và mặt phẳng \(\left( {ACD} \right)\).
Cho hình chóp đều \(S.ABCD\) có tất cả các cạnh bằng \(a\). Tính côsin góc giữa hai mặt phẳng sau:
a) Mặt phẳng \(\left( {SAB} \right)\) và mặt phẳng \(\left( {ABCD} \right)\).
b) Mặt phẳng \(\left( {SAB} \right)\) và mặt phẳng \(\left( {SBC} \right)\).
Cho tứ diện đều ABCD có cạnh bằng a, côsin của góc giữa hai mặt phẳng (ACD) và (BCD) bằng
A. \(\frac{2}{3}\).
B. \(\frac{{\sqrt 3 }}{2}\).
C. \(\frac{{\sqrt 3 }}{3}\).
D. \(\frac{1}{3}\).
Cho tứ diện ABCD có tam giác BCD vuông cân tại B và \(AB \bot \left( {BCD} \right)\). Cho biết \(BC = a\sqrt 2 ,AB = \frac{a}{{\sqrt 3 }}\). Xác định và tính góc giữa hai mặt phẳng (ACD) và (BCD).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a. Cho biết \(SA = a\) và \(SA \bot \left( {ABCD} \right)\). Trên BC lấy điểm I sao cho tam giác SDI vuông tại S. Biết góc giữa hai mặt phẳng (SDI) và (ABCD) là \({60^0}\). Tính độ dài SI.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và \(AB = a\sqrt 2 \). Biết \(SA \bot \left( {ABC} \right)\) và \(SA = a\). Góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A. \({30^0}\)
B. \({45^0}\)
C. \({60^0}\)
D. \({90^0}\)
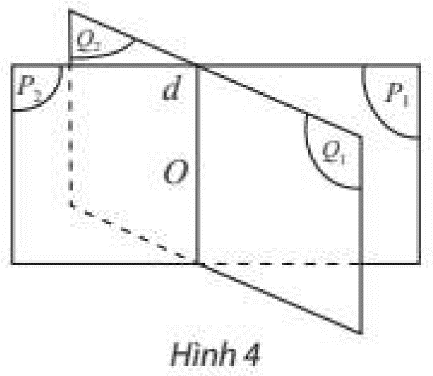
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến \(\Delta \) như hình vẽ. Lấy một điểm O bất kì thuộc đường thẳng \(\Delta \). Gọi m, n là các đường thẳng đi qua O, tương ứng thuôc (P), (Q) và vuông góc với \(\Delta \).
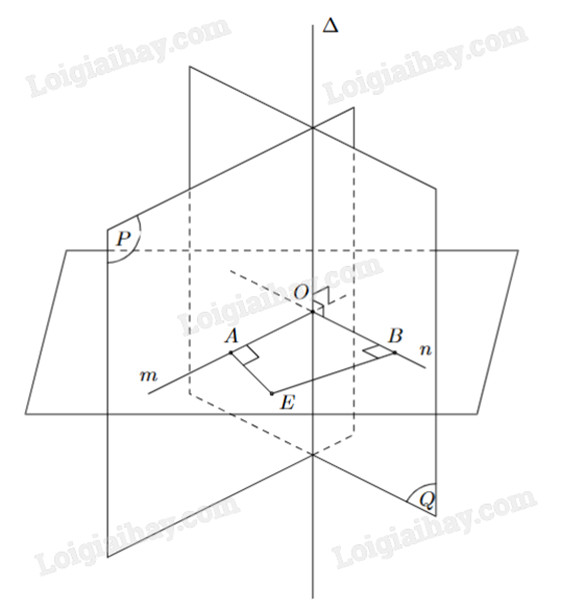
a) Góc giữa hai mặt phẳng (P) và (Q) là góc giữa hai đường thẳng \(\Delta \) và m.
b) Góc giữa hai mặt phẳng (P) và (Q) là góc \(\widehat {AOB}\) (nếu \(\widehat {AOB} < {90^o}\)) hoặc \({180^o} - \widehat {AOB}\) (nếu \({90^o} < \widehat {AOB} < {180^o}\)).
c) Nếu \(\widehat {AOB} = {90^o}\) thì ta nói \((P) \bot (Q)\).
d) Giả sử góc
\(\widehat {AOB} = {120^o}\) thì ta nói góc giữa hai mặt phẳng (P) và (Q) là \({120^o}\).
Cho hình chóp S.ABC có $SA\bot\left( {ABC} \right)$ và $AB\bot BC$. Góc giữa hai mặt phẳng (SBC) và (ABC) là góc nào sau đây?
-
A.
Góc $\widehat{SIA}$ với I là trung điểm của BC.
-
B.
Góc $\widehat{SBA}$ .
-
C.
Góc $\widehat{SCB}$.
-
D.
Góc $\widehat{SCA}$ .







Danh sách bình luận