Đề kiểm tra giữa kì 1 Toán 9 - Đề số 7 có lời giải chi tiết
Đề kiểm tra giữa kì 1 Toán 9 - Đề số 7 có lời giải chi tiết
Đề bài
Bài 1 (2,5 điểm) Cho hai biểu thức
\(A = \frac{{x + 2\sqrt x + 5}}{{\sqrt x - 3}}\) và \(B = \frac{{2\sqrt x - 9}}{{x - 5\sqrt x + 6}} - \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{2\sqrt x + 1}}{{3 - \sqrt x }}\) với \(\left( {x \ge 0,x \ne 4,x \ne 9} \right)\)
a) Tính giá trị của A khi \(x = 16.\)
b) Rút gọn biểu thức \(B\)
c) Biết rằng \(P = A:B\) . Tìm giá trị nhỏ nhất của \(P\)
Bài 2 (3,0 điểm) Giải các phương trình sau:
a) \(\sqrt {x - 5} = 2\)
b) \(\sqrt {{x^2} - 6x + 9} = 5\)
c) \(\sqrt {4{x^2} - 4x + 1} = x + 1\)
d) \(\sqrt {{x^2} - 4x + 4} = \sqrt {4{x^2} - 12x + 9} \)
Bài 3 (3,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) ( \(AB > AC\) ), đường cao \(AH\) ( \(H \in BC\) ). Vẽ phân giác \(AD\) của góc \(BAH\) ( \(D \in BH\) ). Cho \(M\) là trung điểm của \(BA\) .
a) Cho \(AC = 3cm\) ; \(AB = 4cm\) . Hãy giải tam giác \(ABC\) ?(Làm tròn đến độ)
b) Tính diện tích tam giác \(AHC\)
c) Chứng minh rằng: \(\frac{{DH}}{{DB}} = \frac{{HC}}{{AC}}\)
d) Gọi \(E\) là giao điểm của \(DM\) và \(AH\) . Chứng minh: \({S_{\Delta A{\rm{E}}C}} = {S_{\Delta DEC}}\)
Bài 4 (1,0 điểm)
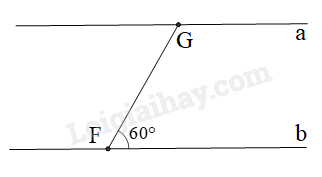
Một con thuyền ở địa điểm \(F\) di chuyển từ bờ sông \(b\) sang bờ sông \(a\) với vận tốc trung bình là \(6\) km/h, vượt qua khúc sông nước chảy mạnh trong \(5\) phút. Biết đường đi của con thuyền là \(FG\) , tạo với bờ sông một góc \(60^\circ \) .
a) Tính \(FG\)
b) Tính chiều rộng của khúc sông (làm tròn đến mét)
-------- Hết --------
Lời giải chi tiết
Bài 1 (2,5 điểm) Cho hai biểu thức
\(A = \frac{{x + 2\sqrt x + 5}}{{\sqrt x - 3}}\) và \(B = \frac{{2\sqrt x - 9}}{{x - 5\sqrt x + 6}} - \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{2\sqrt x + 1}}{{3 - \sqrt x }}\) với \(\left( {x \ge 0,x \ne 4,x \ne 9} \right)\)
a) Tính giá trị của A khi \(x = 16.\)
b) Rút gọn biểu thức \(B\)
c) Biết rằng \(P = A:B\) . Tìm giá trị nhỏ nhất của \(P\)
Phương pháp
a) Kiểm tra \(x = 16\) có thỏa mãn điều kiện hay không, sau đó thay vào biểu thức A để tính.
b) Xác định mẫu thức chung, quy đồng và thực hiện các phép toán với các phân thức đại số.
c) Tính \(P = A:B\) .
Biến đổi P để áp dụng bất đẳng thức Cô si cho 2 số dương \(\sqrt x + 1\) và \(\frac{4}{{\sqrt x + 1}}\) .
Lời giải
a) Ta có \(x = 16\) (thỏa mãn điều kiện), thay vào biểu thức \(A\) ta có:
\(A = \frac{{16 + 2\sqrt {16} + 5}}{{\sqrt {16} - 3}} = \frac{{29}}{1} = 29\)
Vậy khi \(x = 16\) thì \(A = 29\)
b) Ta có:
\(\begin{array}{l}B = \frac{{2\sqrt x - 9}}{{x - 5\sqrt x + 6}} - \frac{{\sqrt x + 3}}{{\sqrt x - 2}} - \frac{{2\sqrt x + 1}}{{3 - \sqrt x }}\\ = \frac{{2\sqrt x - 9}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} - \frac{{\sqrt x + 3}}{{\sqrt x - 2}} + \frac{{2\sqrt x + 1}}{{\sqrt x - 3}}\\ = \frac{{2\sqrt x - 9 - \left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right) + \left( {2\sqrt x + 1} \right)\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\ = \frac{{2\sqrt x - 9 - x + 9 + 2x - 3\sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}}\\ = \frac{{x - \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 3} \right)}} = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\end{array}\)
Vậy \(B = \frac{{\sqrt x + 1}}{{\sqrt x - 3}}\) , \(\left( {x \ge 0,x \ne 4,x \ne 9} \right)\)
c) Ta có \(P = A:B = \frac{{x + 2\sqrt x + 5}}{{\sqrt x - 3}}:\frac{{\sqrt x + 1}}{{\sqrt x - 3}} = \frac{{x + 2\sqrt x + 5}}{{\sqrt x + 1}} = \frac{{{{\left( {\sqrt x + 1} \right)}^2} + 4}}{{\sqrt x + 1}} = \sqrt x + 1 + \frac{4}{{\sqrt x + 1}}\)
Do \(x \ge 0 \Rightarrow \sqrt x \ge 0 \Rightarrow \sqrt x + 1 > 0\)
Áp dụng bất đẳng thức Cô si cho 2 số dương \(\sqrt x + 1\) và \(\frac{4}{{\sqrt x + 1}}\) ta có:
\(P = \sqrt x + 1 + \frac{4}{{\sqrt x + 1}} \ge 2\sqrt {\left( {\sqrt x + 1} \right)\frac{4}{{\sqrt x + 1}}} = 4\)
Dấu bằng xảy ra \( \Leftrightarrow \sqrt x + 1 = \frac{4}{{\sqrt x + 1}} \Leftrightarrow \sqrt x + 1 = 2 \Leftrightarrow \sqrt x = 1 \Leftrightarrow x = 1\) (thỏa mãn điều kiện)
Vậy \(\min P = 4\) khi \(x = 1\)
Bài 2 (3,0 điểm) Giải các phương trình sau:
a) \(\sqrt {x - 5} = 2\)
b) \(\sqrt {{x^2} - 6x + 9} = 5\)
c) \(\sqrt {4{x^2} - 4x + 1} = x + 1\)
d) \(\sqrt {{x^2} - 4x + 4} = \sqrt {4{x^2} - 12x + 9} \)
Phương pháp
Xác định điều kiện xác định của phương trình.
a) Bình phương hai vế để tìm x.
b) Đưa về phương trình trị tuyệt đối chia hai trường hợp
c) Bình phương hai vế để tìm x.
d) Đưa các hệ số ra ngoài căn và sử dụng hằng đẳng thức, đưa về phương trình thuyệt đối để chia hai trường hợp.
Lời giải
a) \(\sqrt {x - 5} = 2\) .
Điều kiện xác định \(x \ge 5\)
Ta có: \(\sqrt {x - 5} = 2 \Leftrightarrow x - 5 = 4 \Leftrightarrow x = 9\) (thỏa mãn \(x \ge 5\) )
Vậy tập nghiệm của phương trình là \(S = \left\{ 9 \right\}\) .
b) \(\sqrt {{x^2} - 6x + 9} = 5\)
Ta có: \(\sqrt {{x^2} - 6x + 9} = 5 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2}} = 5 \Leftrightarrow \left| {x - 3} \right| = 5 \Leftrightarrow \left[ \begin{array}{l}x - 3 = 5\\x - 3 = - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 8\\x = - 2\end{array} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {8; - 2} \right\}\) .
c) \(\sqrt {4{x^2} - 4x + 1} = x + 1\)
Ta có: \(\sqrt {4{x^2} - 4x + 1} = x + 1 \Leftrightarrow \sqrt {{{\left( {2x - 1} \right)}^2}} = x + 1 \Leftrightarrow \left| {2x - 1} \right| = x + 1 \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\\left[ \begin{array}{l}2x - 1 = x + 1\\2x - 1 = - x - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\\left[ \begin{array}{l}x = 2\,\left( {{\rm{tm}}} \right)\\x = 0\,\left( {{\rm{tm}}} \right)\end{array} \right.\end{array} \right.\) Vậy tập nghiệm của phương trình là \(S = \left\{ {2;0} \right\}\) .
d) \(\sqrt {{x^2} - 4x + 4} = \sqrt {4{x^2} - 12x + 9} \)
Ta có: \(\sqrt {{x^2} - 4x + 4} = \sqrt {4{x^2} - 12x + 9} \Leftrightarrow \sqrt {{{\left( {x - 2} \right)}^2}} = \sqrt {{{\left( {2x - 3} \right)}^2}} \Leftrightarrow \left| {x - 2} \right| = \left| {2x - 3} \right|\) \( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 2x - 3\\x - 2 = - 2x + 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - x = - 1\\3x = 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \frac{5}{3}\end{array} \right.\)
Vậy tập nghiệm của phương trình là \(S = \left\{ {1;\frac{5}{3}} \right\}\) .
Bài 3 (3,5 điểm) Cho tam giác \(ABC\) vuông tại \(A\) ( \(AB > AC\) ), đường cao \(AH\) ( \(H \in BC\) ). Vẽ phân giác \(AD\) của góc \(BAH\) ( \(D \in BH\) ). Cho \(M\) là trung điểm của \(BA\) .
a) Cho \(AC = 3cm\) ; \(AB = 4cm\) . Hãy giải tam giác \(ABC\) ? (Làm tròn đến độ)
b) Tính diện tích tam giác \(AHC\)
c) Chứng minh rằng: \(\frac{{DH}}{{DB}} = \frac{{HC}}{{AC}}\)
d) Gọi \(E\) là giao điểm của \(DM\) và \(AH\) . Chứng minh: \({S_{\Delta A{\rm{E}}C}} = {S_{\Delta DEC}}\)
Phương pháp
a) Sử dụng định lí Pytago cho tam giác vuông ABC để tính BC. Sử dụng tỉ số lượng giác để tính góc B, góc C.
b) Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\) , đường cao \(AH\) ta có: \(AH.BC = AB.AC\) ta tính được AH; \(A{C^2} = CH.BC\) ta tính được CH. Sử dụng công thức tính diện tích tam giác ABC: \({S_{\Delta ABC}} = \frac{1}{2}HC.AH\) .
c) Dựa vào tính chất đường phân giác và ΔAHB ∽ ΔCHA (g-g) suy ra các tỉ số bằng nhau của các cạnh tương ứng.
d) Kẻ HG // AB.
Chứng minh \(\frac{{DH}}{{DB}} = \frac{{HC}}{{AC}} = \frac{{HC}}{{DC}}\) và \(\frac{{EH}}{{EA}} = \frac{{DH}}{{DB}}\) suy ra \(\frac{{HC}}{{DC}} = \frac{{HE}}{{AE}} \Rightarrow HC.AE = DC.HE\) .
Chứng minh \(\frac{{{S_{ACE}}}}{{{S_{DEC}}}}\) = 1.
Lời giải
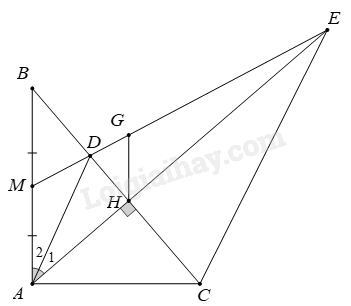
a) Xét \(\Delta ABC\) vuông tại \(A\) (gt) có:
\(A{B^2} + A{C^2} = B{C^2}\) (định lí Pytago)
\( \Rightarrow {4^2} + {3^2} = B{C^2}\)
\( \Rightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5\) (cm)
Ta có: \(\sin B = \frac{{AC}}{{BC}} = \frac{3}{5} \Rightarrow \widehat B \approx 37^\circ \)
\(\widehat B + \widehat C = 90^\circ \)
\( \Rightarrow \widehat C \approx 53^\circ \)
b) Áp dụng hệ thức lượng vào \(\Delta ABC\) vuông tại \(A\) , đường cao \(AH\) ta có: \(AH.BC = AB.AC\)
\( \Leftrightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{4.3}}{5} = 2,4\) (cm)
Lại có: \(A{C^2} = CH.BC \Leftrightarrow CH = \frac{{{3^2}}}{{BC}} = \frac{9}{5} = 1,8\) (cm)
Diện tích tam giác \(AHC\) là:
\(\frac{1}{2}.HC.AH = \frac{1}{2}.2,4.1,8 = 2,16\left( {c{m^2}} \right)\)
c) Xét \(\Delta ABH\) có phân giác \(AD\) (giả thuyết)
\( \Rightarrow \frac{{DH}}{{DB}} = \frac{{AH}}{{AB}}\) (tính chất phân giác trong tam giác)
ΔAHB ∽ ΔCHA (g-g)
\( \Rightarrow \frac{{AH}}{{AB}} = \frac{{HC}}{{AC}}\) (hai góc tương ứng)
\( \Rightarrow \frac{{DH}}{{DB}} = \frac{{HC}}{{AC}}\left( { = \frac{{AH}}{{AB}}} \right)\) (đpcm)
d) Kẻ \(HG\,{\rm{//}}\,AB\)
Xét \(\Delta ABD\) có \(\widehat {ADC}\) là góc ngoài \( \Rightarrow \widehat {ADC} = \widehat {ABD} + \widehat {{A_2}}\)
Mà \(\widehat {DAC} = \widehat {{A_1}} + \widehat {HAC}\)
Lại có \(\widehat {ABD} = \widehat {HAC}\)
\( \Rightarrow \widehat {ADC} = \widehat {DAC}\)
\( \Rightarrow \Delta ACD\) cân tại \(C\) (dhnb)
\( \Rightarrow AC = DC\) (tính chất)
\( \Rightarrow \frac{{DH}}{{DB}} = \frac{{HC}}{{AC}} = \frac{{HC}}{{DC}}\) (1)
Xét \(\Delta AEM\) , có \(GH\,{\rm{//}}\,AB\) \( \Rightarrow \frac{{EH}}{{EA}} = \frac{{HG}}{{AM}}\) (định lí Ta lét)
Vì \(M\) là trung điểm của \(AB\) (gt) \( \Rightarrow AM = BM\) \( \Rightarrow \frac{{EH}}{{EA}} = \frac{{HG}}{{BM}}\)
Xét \(\Delta DGH\) , có \(GH//AB\) \( \Rightarrow \frac{{DH}}{{DB}} = \frac{{HG}}{{BM}}\) (định lí Ta lét)
\( \Rightarrow \frac{{EH}}{{EA}} = \frac{{DH}}{{DB}}\) (2)
Từ \((1);(2) \Rightarrow \frac{{HC}}{{DC}} = \frac{{HE}}{{AE}} \Rightarrow HC.AE = DC.HE\)
Ta có \({S_{ACE}} = \frac{1}{2}CH.AE\) , \({S_{DEC}} = \frac{1}{2}EH.DC\)
\( \Rightarrow \frac{{{S_{ACE}}}}{{{S_{DEC}}}} = \frac{{CH.AE}}{{EH.DC}} = 1\)
Vậy \({S_{\Delta A{\rm{E}}C}} = {S_{\Delta DEC}}\)
Bài 4 (1,0 điểm)
Một con thuyền ở địa điểm \(F\) di chuyển từ bờ sông \(b\) sang bờ sông \(a\) với vận tốc trung bình là \(6\) km/h, vượt qua khúc sông nước chảy mạnh trong \(5\) phút. Biết đường đi của con thuyền là \(FG\) , tạo với bờ sông một góc \(60^\circ \) .
a) Tính \(FG\)
b) Tính chiều rộng của khúc sông (làm tròn đến mét)
Phương pháp
a) Độ dài FG là quãng đường con thuyền đi được: S = v.t.
b) Kẻ GH \( \bot \) b tại H. GH chính là chiều rộng của khúc sông. Sử dụng định nghĩa tỉ số lượng giác của góc nhọn để suy ra chiều rộng của khúc sông.
Lời giải
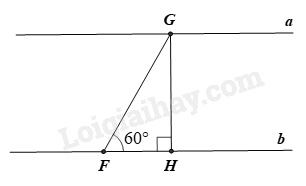
a) \(FG\) là quãng đường đi được của thuyền. \(FG = 6.\frac{5}{{60}} = 0,5\,km = 500\,m\) .
b) Gọi \(GH\) là chiều rộng của khúc sông.
Xét \(\Delta GHF\) vuông tại H, áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có: \(GH = FG.\sin \widehat {GFB} = 500.\sin 60^\circ = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 \approx 433\) m.
Vậy, chiều rộng của khúc sông xấp xỉ \(433\) m.
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 8 có lời giải chi tiết
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 9 có lời giải chi tiết
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 10 có lời giải chi tiết
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 11 có lời giải chi tiết
- Đề kiểm tra giữa kì 1 Toán 9 - Đề số 12 có lời giải chi tiết
>> Xem thêm












