Câu 8 trang 121 SGK Hình học 11 Nâng cao

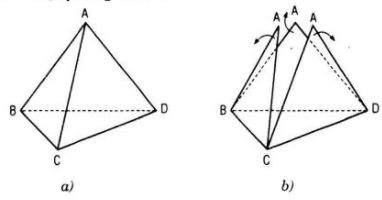
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).

Đề bài

Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A₁BC, A₂CD, A₃BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).

Lời giải chi tiết

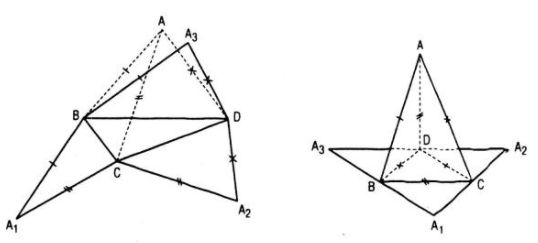
Ta có hình khai triển của tứ diện ABCD trên mp(BCD) là tam giác A₁A₂A₃.

Ta chỉ cần chứng minh tam giác A₁A₂A₃ có ba góc nhọn.

Thật vậy, xét tam giác AA₁A₂có AC = A₁C = A₂C nên AA₁ ⊥ AA₂. Lí luận tương tự như trên, ta có AA₁, AA₂, AA₃ đôi một vuông góc, từ đó tứ diện AA₁A₂A₃ có mặt A₁A₂A₃ là tam giác có ba góc nhọn.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.3 trên 6 phiếu

Bài tiếp theo

Câu 7 trang 121 SGK Hình học 11 Nâng cao
Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :
Câu 6 trang 120 SGK Hình học 11 Nâng cao
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABB’A’ là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB’.
Câu 5 trang 120 SGK Hình học 11 Nâng cao
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
Câu 4 trang 120 SGK Hình học 11 Nâng cao
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng
Câu 3 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
Câu 2 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABC có SA = Sb = SC = a,
Câu 1 trang 120 SGK Hình học 11 Nâng cao
Tứ diện OABC có OA = OB = OC = a và