Câu 47 trang 75 SGK Hình học 11 Nâng cao

Cho hình hộp ABCD.A1B1C1D1. Tìm điểm I trên đường chéo B1D và điểm J trên đường chéo AC sao cho IJ // BC1. Tính tỉ số

Đề bài

Cho hình hộp ABCD.A₁B₁C₁D₁. Tìm điểm I trên đường chéo B₁D và điểm J trên đường chéo AC sao cho IJ // BC₁. Tính tỉ số \({{ID} \over {I{B_1}}}\)

Lời giải chi tiết

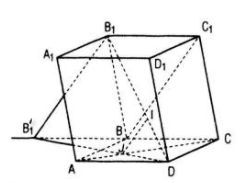
Giả sử, ta tìm được I ∈ B₁D, J ∈ AC sao cho IJ // BC₁

Xét phép chiếu song song theo phương BC₁ lên mp(ABCD). Khi đó hình chiếu của các điểm I , D, B₁ lần lượt là J, D , B₁’

Do D, I ,B₁ thẳng hàng nên D, J, B₁’ thẳng hàng

Vậy J chính là giao điểm của hai đường thẳng B’₁D và AC. Từ đó ta có thể tìm I, J như sau:

- Dựng B’₁ là hình chiếu B₁ qua phép chiếu song song ở trên (BC₁B₁B’₁ là hình bình hành)

- Dựng J là giao điểm của B’₁D với AC

- Trong mp(B₁B’₁D) kẻ JI song song với B₁B’₁ cắt B₁D tại I

Rõ ràng I và J thỏa mãn điều kiện của bài toán

Dễ thấy B’₁ thuộc đường thẳng BC và \(AD = {1 \over 2}B{'_1}C\)

Từ đó suy ra : \({{ID} \over {I{B_1}}} = {{ID} \over {JB{'_1}}} = {{AD} \over {B{'_1}C}} = {1 \over 2}\)

Vậy ta có: \({{ID} \over {I{B_1}}} = {1 \over 2}\)

Loigiaihay.com

👉

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Câu 46 trang 75 SGK Hình học 11 Nâng cao
Vẽ hình biểu diễn của một lục giác đều
Câu 45 trang 75 SGK Hình học 11 Nâng cao
Vẽ hình biểu diễn của một hình vuông nội tiếp trong một đường tròn
Câu 44 trang 75 SGK Hình học 11 Nâng cao
Vẽ hình biểu diễn của một tam giác vuông nội tiếp trong một đường tròn
Câu 43 trang 75 SGK Hình học 11 Nâng cao
Vẽ hình biểu diễn của một tứ diện và trọng tâm của nó
Câu 42 trang 74 SGK Hình học 11 Nâng cao
Tam giác ABC có hình chiếu song song là tam giác A’B’C’. Chứng minh rằng trọng tâm tam giác ABC có hình chiếu song song là trọng tâm tam giác A’B’C’
Câu 41 trang 74 SGK Hình học 11 Nâng cao
Trong các mệnh đề sau, mệnh đề nào đúng ?
Câu 40 trang 74 SGK Hình học 11 Nâng cao
Trong các mệnh đề sau, mệnh đề nào đúng ?