Câu 29 trang 117 SGK Hình học 11 Nâng cao

Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.

Đề bài

Cho tứ diện ABCD có AC = BC = AD = BD = a, AB = c, CD = c’. Tính khoảng cách giữa hai đường thẳng AB và CD.

Lời giải chi tiết

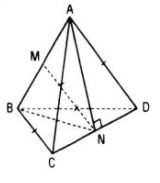
Gọi M, N lần lượt là trung điểm của AB và CD

ΔACD cân nên AN ⊥ CD và ΔBCD cân nên BN ⊥ CD.

Do đó CD ⊥ (ABN) suy ra CD ⊥ MN.

Tương tự ta cũng có AB ⊥ MN

Vậy d(AB, CD) = MN

Ta có:

\(\eqalign{ & M{N^2} = A{N^2} - A{M^2} = A{D^2} - N{D^2} - A{M^2} \cr & = {a^2} - {{c{'^2}} \over 4} - {{{c^2}} \over 4} = {1 \over 4}\left( {4{a^2} - c{'^2} - {c^2}} \right) \cr} \)

Vậy \(MN = {1 \over 2}\sqrt {4{a^2} - c{'^2} - {c^2}} \) với điều kiện \(4{a^2} > {c^2} + c{'^2}\)

Loigiaihay.com

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 4 phiếu

Bài tiếp theo

Câu 30 trang 117 SGK Hình học 11 Nâng cao
Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh đều bằng a. Góc tạo bởi cạnh bên và mặt đáy bằng 30˚. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’.
Câu 31 trang 117 SGK Hình học 11 Nâng cao
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’
Câu 32 trang 117 SGK Hình học 11 Nâng cao
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a, AC’ = 2a. a. Tính khoảng cách từ điểm D đến mặt phẳng (ACD’) b. Tìm đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng cách giữa hai đường thẳng ấy.
Câu 33 trang 118 SGK Hình học 11 Nâng cao
Cho hình hộp thoi ABCD.A’B’C’D’ có các cạnh đều bằng a và Tính khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’).
Câu 34 trang 118 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình chữ nhật và Ab = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng
Câu 35 trang 118 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Chứng minh rằng nếu AC = BD, AD = BC thì đường vuông góc chung của AB và CD là đường thẳng nối trung điểm của AB và CD. Điều ngược lại có đúng không ?