-
Toán 11 tập 1 - Cùng khám phá
-
Giải Toán 11 tập 2 - Cùng khám phá
Bài 8.28 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
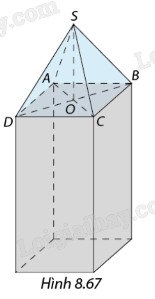
Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp từ giác như hình 867
Đề bài
Để chuẩn bị cho một buổi triển lãm quốc tế, các trang sức có giá trị lớn được đặt bảo mật trong các khối chóp từ giác như hình 867 và đặt trên phía trên một trụ hình hộp chữ nhật có độ cao 1 m, đây là hình vuông cạnh 50 cm. Ban tổ chức sự kiện dự định dùng các tấm kính cường lực hình tam giác còn có cạnh bên là 60 cm để ráp lại thành khối chóp nói trên. Tỉnh khoảng cách tử đỉnh hình chóp đến mặt sàn nơi diễn ra buổi triển lãm.
Phương pháp giải - Xem chi tiết
Để tìm khoảng cách tử đỉnh hình chóp đến mặt sàn nơi diễn ra buổi triển lãm ta cần tìm độ dài SO.
Lời giải chi tiết
ABCD là hình vuông có cạnh 50 cm nên BD = \(50\sqrt 2 \). Suy ra DO = \(25\sqrt 2 \)
Khoảng cách từ đỉnh hình chóp đến mặt sàn là: \(100 + SO = 100 + \sqrt {S{D^2} - O{D^2}} = 100 + \sqrt {{{60}^2} - {{\left( {25\sqrt 2 } \right)}^2}} \approx 148\)
Bình luận
Chia sẻ
- Bài 8.27 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.26 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.25 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.24 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
- Bài 8.23 trang 79 SGK Toán 11 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
