-
SBT TOÁN TẬP 1 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
-
SBT TOÁN TẬP 2 - KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Giải bài 4.56 trang 69 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
Cho tam giác ABC đều các cạnh có độ dài bằng 1
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Cho tam giác \(ABC\) đều các cạnh có độ dài bằng 1. Lấy \(M,\,\,N,\,\,P\) tương ứng thuộc các cạnh \(BC,\,\,CA,\,\,AB\) sao cho \(BM = 2MC,\,\,CN = 2NA\) và \(AM \bot NP.\) Tỉ số của \(\frac{{AP}}{{AB}}\) bằng
A. \(\frac{5}{{12}}\)
B. \(\frac{7}{{12}}\)
C. \(\frac{5}{7}\)
D. \(\frac{7}{5}\)
Phương pháp giải - Xem chi tiết
- Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)
- Biểu diễn các vectơ \(\overrightarrow {PN} \) và \(\overrightarrow {AM} \) theo các vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)
- Tìm x dựa vào tích vô hướng của hai vectơ \(\overrightarrow {AM} .\overrightarrow {PN} = 0\)
Lời giải chi tiết
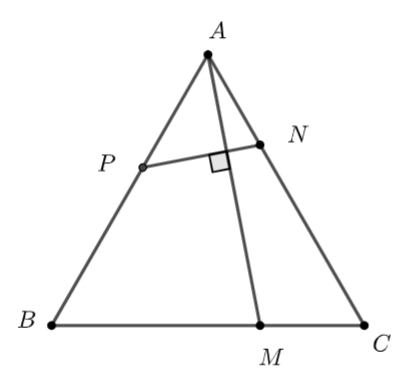
Đặt \(AP = x\) \(\left( {0 < x < 1} \right)\)
Ta có: \(\overrightarrow {PN} = \overrightarrow {PA} + \overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} - x\overrightarrow {AB} \)
Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} \)
Ta có: \(AM \bot PN\) \( \Rightarrow \) \(\overrightarrow {AM} .\overrightarrow {PN} = 0\)
\( \Leftrightarrow \) \(\left( {\frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} } \right).\left( {\frac{1}{3}\overrightarrow {AC} - x\overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \) \(\frac{1}{9}\overrightarrow {AB} .\overrightarrow {AC} - \frac{x}{3}{\overrightarrow {AB} ^2} + \frac{2}{9}{\overrightarrow {AC} ^2} - \frac{{2x}}{3}\overrightarrow {AC} .\overrightarrow {AB} = 0\)
\( \Leftrightarrow \) \(\frac{1}{9}.\frac{1}{2} - \frac{x}{3} + \frac{2}{9} - \frac{{2x}}{3}.\frac{1}{2} = 0\)
\( \Leftrightarrow \) \(\frac{1}{{18}} - \frac{x}{3} + \frac{2}{9} - \frac{x}{3} = 0\)
\( \Leftrightarrow \) \(1 - 6x + 4 - 6x = 0\)
\( \Leftrightarrow \) \(12x = 5\) \( \Leftrightarrow \) \(x = \frac{5}{{12}}\)
Vậy \(\frac{{AP}}{{AB}} = \frac{5}{{12}}\)
Chọn A.
Bình luận
Chia sẻ
- Giải bài 4.57 trang 69 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 4.58 trang 69 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 4.59 trang 69 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 4.60 trang 70 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
- Giải bài 4.61 trang 70 sách bài tập toán 10 - Kết nối tri thức với cuộc sống
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Kết nối tri thức - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
