Giải bài 4 (4.32) trang 77 vở thực hành Toán 7

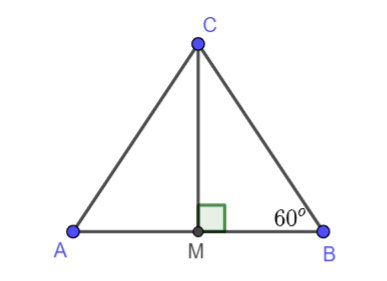
Bài 4 (4.32). Cho tam giác MBC vuông tại M có \(\widehat B = {60^o}\). Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Đề bài

Bài 4 (4.32). Cho tam giác MBC vuông tại M có \(\widehat B = {60^o}\). Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Phương pháp giải - Xem chi tiết

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.

Lời giải chi tiết

\(\Delta MBC,\widehat M = {90^o},\widehat B = {60^o},MA = MB\)

A thuộc tia đối của tia MB

\(\Delta ABC\)đều.

Ta thấy hai tam giác MBC và MAC vuông tại M và có:

MB = MA (theo giả thiết)

MC là cạnh chung

Vậy \(\Delta MBC = \Delta MAC\)(hai cạnh góc vuông). Do đó \(\widehat A = \widehat B = {60^o}\)

Suy ra \(\widehat C = {180^o} - \widehat A - \widehat B = {60^o}\)

Vậy ABC là tam giác có ba góc bằng nhau nên đây là tam giác đều.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5 trang 77 vở thực hành Toán 7
Bài 5. Cho tam giác ABC cân tại A. Gọi M, N lần lượt là trung điểm AB, AC. Gọi O là giao diểm của đường thẳng BN và CM. Chứng minh rằng O nằm trên đường trung trực của đoạn thẳng BC.
Giải bài 6 trang 78 vở thực hành Toán 7
Bài 6. Cho hình chữ nhật ABCD và cho M là trung điểm của đoạn thẳng AB như hình vẽ dưới đây. Chứng minh rằng M nằm trên đường trung trực của CD.
Giải bài 3 (4.31) trang 76 vở thực hành Toán 7
Bài 3 (4.31). Cho năm điểm A, B,C,D,O như hình vẽ. Biết rằng OA = OB, OC = OD. a) Chứng minh rằng AC=BD. b) Chứng minh rằng \(\Delta ACD = \Delta BDC\)
Giải bài 2 (4.30) trang 76 vở thực hành Toán 7
Bài 2 (4.30). Cho góc xOy. Trên tia Ox lấy hai điểm A, M, trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM.Chứng minh rằng: a) \(\Delta OAN = \Delta OBM\) b) \(\Delta AMN = \Delta BNM\)
Giải bài 1 (4.29) trang 76 vở thực hành Toán 7
Bài 1 (4.29). Cho các điểm A, B, C, D như hình vẽ dưới đây. Tính các độ dài a, b và các số đo góc x, y.