 Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
 Bài tập cuối chương 4 trang 78, 79, 80, 81 Vở thực hành..
Bài tập cuối chương 4 trang 78, 79, 80, 81 Vở thực hành..
Giải bài 2 (4.34) trang 79 vở thực hành Toán 7
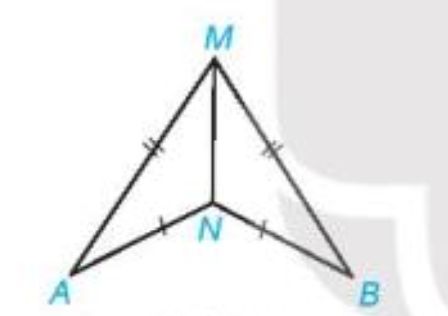
Bài 2 (4.34). Trong hình vẽ sau, ta có AM = BM, AN = BN. Chứng minh rằng \(\widehat {MAN} = \widehat {MBN}\)
Tổng hợp đề thi học kì 1 lớp 7 tất cả các môn - Kết nối tri thức
Toán - Văn - Anh - Khoa học tự nhiên...
Đề bài
Bài 2 (4.34). Trong hình vẽ sau, ta có AM = BM, AN = BN. Chứng minh rằng
\(\widehat {MAN} = \widehat {MBN}\)
Phương pháp giải - Xem chi tiết
Chứng minh hai tam giác MAN và MBN bằng nhau
Lời giải chi tiết
Xét hai tam giác MAN và MBN có:
AM = BM (theo giả thiết)
AN = BN (theo giả thiết)
MN là cạnh chung
Vậy \(\Delta MAN = \Delta MBN\)(c-c-c). Suy ra \(\widehat {MAN} = \widehat {MBN}\)
- Giải bài 3 (4.35) trang 79 vở thực hành Toán 7
- Giải bài 4 (4.36) trang 79 vở thực hành Toán 7
- Giải bài 5 (4.38) trang 79 vở thực hành Toán 7
- Giải bài 6 (4.39) trang 80 vở thực hành Toán 7
- Giải bài 7 trang 80 vở thực hành Toán 7
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục











