Cách tính khoảng cách từ điểm đến đường thẳng - Toán 11

1. Định nghĩa khoảng cách từ điểm đến đường thẳng

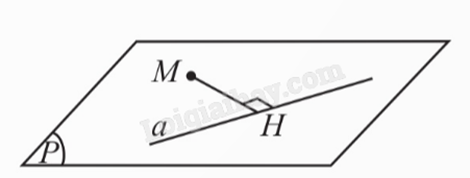
Nếu H là hình chiếu vuông góc của điểm M trên đường thẳng a thì độ dài đoạn MH được gọi là khoảng cách từ M đến đường thẳng a, kí hiệu d(M, a).

Quy ước: \(d(M,a) = 0 \Leftrightarrow M \in a\).

2. Cách tính khoảng cách từ điểm đến đường thẳng

Cách tính khoảng cách từ điểm M đến đường thẳng a:

B1: Xác định hình chiếu vuông góc H của M trên a.

B2: Tính MH.

Ví dụ minh hoạ:

Cho đoạn thẳng MN có độ dài a và đường thẳng \(\Delta \) đi qua N sao cho góc giữa hai đường thẳng MN và \(\Delta \) là \(\varphi \) (\({0^o} < \varphi < {90^o}\)). Tính khoảng cách từ M đến \(\Delta \) theo \(a,\varphi \).

Giải:

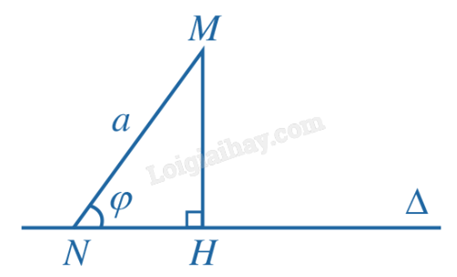
Gọi H là hình chiếu của M trên đường thẳng \(\Delta \). Khi đó \(d(M,\Delta ) = MH.\) Vì góc giữa hai đường thẳng MN và \(\Delta \) là \(\varphi \) nên \(\widehat {MNH} = \varphi .\)

Suy ra \(MH = MN \cdot \sin \varphi = a\sin \varphi .\) Vậy \(d(M,\Delta ) = a\sin \varphi .\)

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE

Cách tính khoảng cách từ điểm đến đường thẳng - Toán 11

1. Định nghĩa khoảng cách từ điểm đến đường thẳng

2. Cách tính khoảng cách từ điểm đến đường thẳng

Xem thêm kho từ điển