Cách tính khoảng cách giữa hai đường thẳng song song - Toán 11

Khoảng cách giữa hai đường thẳng song song \(\Delta \), \(\Delta '\) là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, kí hiệu \(d(\Delta ,\Delta ')\).

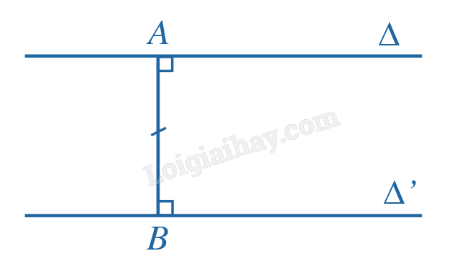
Trong hình, ta có \(d(\Delta ,\Delta ') = AB\) với \(A \in \Delta \), \(B \in \Delta '\), \(AB \bot \Delta \), \(AB \bot \Delta '\) và \(\Delta //\Delta '\).

Để tính khoảng cách giữa hai đường thẳng song song \(\Delta \), \(\Delta '\), ta thực hiện:

B1: Lấy một điểm A bất kì thuộc \(\Delta \).

B2: Xác định hình chiếu vuông góc B của A trên \(\Delta '\).

B3: Khi đó \(d(\Delta ,\Delta ') = AB\). Tính AB.

Ví dụ minh hoạ:

Cho hình hộp ABCD.A'B'C'D' có AA' = a, góc giữa hai đường thẳng AB và DD' bằng \({60^o}\). Tính khoảng cách giữa hai đường thẳng AB và A'B'.

Giải:

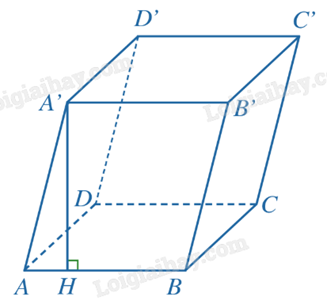
Gọi H là hình chiếu vuông góc của A' trên AB. Do AB // A'B' nên d(AB, A'B') = A'H.

Vì AA' // DD' nên góc giữa đường thẳng AB và AA' bằng góc giữa đường thẳng AB và DD'. Suy ra \(\widehat {A'AH} = {60^o}\).

Trong tam giác vuông A'AH có:

\(A'H = AA'.\sin \widehat {A'AH} = a\sin {60^o} = \frac{{a\sqrt 3 }}{2}\).

Vậy \(d(AB,A'B') = \frac{{a\sqrt 3 }}{2}\).