Cách tính khoảng cách giữa đường thẳng và mặt phẳng song song - Toán 11

Cho đường thẳng \(\Delta \) song song với mặt phẳng (P). Khoảng cách giữa đường thẳng \(\Delta \) và mặt phẳng (P) là khoảng cách từ một điểm bất kì thuộc đường thẳng \(\Delta \) đến mặt phẳng (P), kí hiệu \(d\left( {\Delta ,(P)} \right)\).

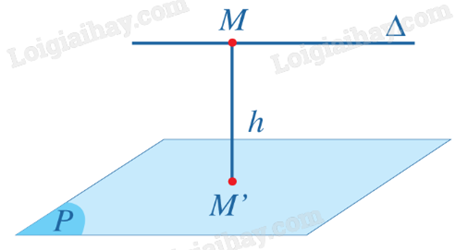
Trong hình, ta có \(d\left( {\Delta ,(P)} \right) = MM' = h\), trong đó \(M \in \Delta \), \(M' \in (P)\), \(MM' \bot (P)\) và \(\Delta //(P)\).

Để tính khoảng cách giữa đường thẳng \(\Delta \) song song với mặt phẳng (P), ta thực hiện:

B1: Lấy điểm M bất kì trên \(\Delta \).

B2: Xác định hình chiếu vuông góc M’ của M trên (P).

B3: Khi đó \(d\left( {\Delta ,(P)} \right) = MM' = h\). Tính MM’.

Ví dụ minh hoạ:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA \perp (ABCD). Chứng minh CD // (SAB) và tính khoảng cách giữa CD và mặt phẳng (SAB).

Giải:

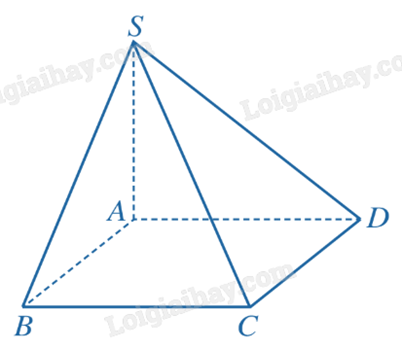
Do \(CD//AB\), \(AB \subset (SAB)\), \(CD\not  \subset (SAB)\) nên \(CD//(SAB)\).

Vì \(D \in CD\) nên \(d(CD,(SAB)) = d(D,(SAB))\).

Do \(SA \bot (ABCD)\), \(DA \subset (ABCD)\) nên \(SA \bot DA\).

Vì DA vuông góc với hai đường thẳng AB, SA cắt nhau trong (SAB) nên \(DA \bot (SAB)\).

Do đó \(d(D,(SAB)) = DA = a\). Vậy \(d(CD,(SAB)) = a\).