Cách tính khoảng cách giữa hai đường thẳng chéo nhau - Toán 11

Cho hai đường thẳng a, b chéo nhau.

- Đường thẳng \(\Delta \) vừa vuông góc, vừa cắt cả hai đường thẳng a và b được gọi là đường vuông góc chung của hai đường thẳng đó.

- Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng \(\Delta \) với hai đường thẳng a, b được gọi là đoạn vuông góc chung của hai đường thẳng đó.

- Độ dài đoạn vuông góc chung của hai đường thẳng a, b gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b, kí hiệu \(d(a,b)\).

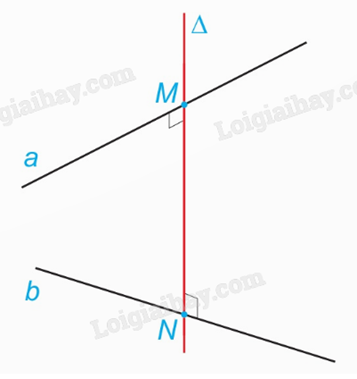
Trong hình, ta có \(d(a,b) = MN\).

Để tính khoảng cách giữa hai đường thẳng chéo nhau a và b, ta thực hiện:

TH1: a không vuông góc với b.

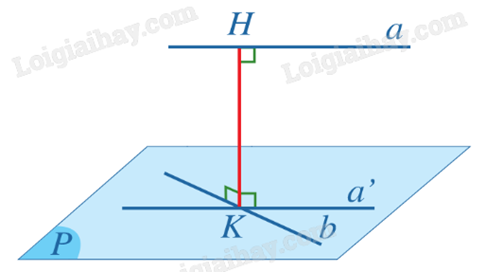
- B1: Xác định mặt phẳng (P) chứa b và song song với a.

- B2: Xác định hình chiếu vuông góc a’ của a trên (P).

- B3: Xác định giao điểm K của a’ và b.

- B4: Xác định hình chiếu vuông góc H của K trên a.

- B4: Khi đó, \(d(a,b) = d\left( {a,(P)} \right) = HK\). Tính HK.

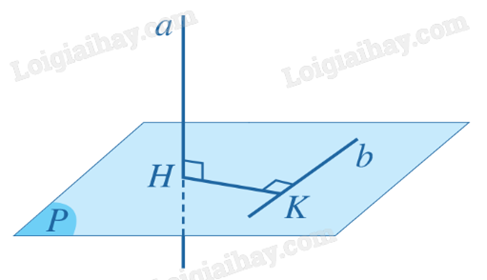
TH2: a vuông góc với b.

- B1: Xác định mặt phẳng (P) chứa b và vuông góc với a.

- B2: Xác định giao điểm H của a và (P).

- B3: Xác định hình chiếu vuông góc K của H trên b.

- B4: Khi đó, \(d(a,b) = HK\).

Ví dụ minh hoạ:

1) Cho lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình vuông cạnh 2a, O là giao điểm của AC và BD, AA’ = a, AA’ vuông góc với mặt phẳng chứa đáy. Tính:

a) \(d(AC,A'B')\);

b) \(d(CC',BD)\).

Giải:

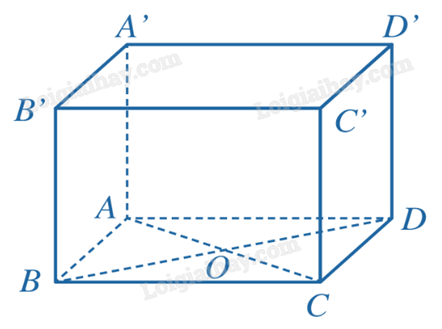
a) Vì AA’ vuông góc với cả hai mặt phẳng (ABCD) và (A’B’C’D’) nên AA’ ⊥ AC, AA’ ⊥ A’B’. Suy ra đoạn thẳng AA’ là đoạn vuông góc chung của AC và A’B’.

Vậy \(d(AC,A'B') = AA' = a\).

b) Vì CC’ vuông góc với (ABCD) nên CC’ ⊥ OC. Do đáy ABCD là hình vuông có O là giao điểm của AC và BD nên BD ⊥ OC. Suy ra đoạn thẳng OC là đoạn vuông góc chung của CC’ và BD.

Vậy \(d(CC',BD) = OC = a\sqrt 2 \).

2) Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD). Tính khoảng cách giữa hai đường thẳng:

a) SB và CD;

b) AB và SC.

Giải:

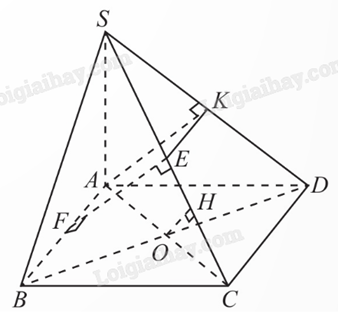
a) Ta có BC ⊥ SA và BC ⊥ AB, suy ra BC ⊥ SB.

Mặt khác BC ⊥ CD, suy ra BC là đoạn vuông góc chung của hai đường SB và CD. Ta có \(d(SB,CD) = BC = a\).

b) Cách 1. Ta có \(AB \bot (SAD)\) và SD là hình chiếu vuông góc của SC lên (SAD). Vẽ \(AK \bot SD\), KE // AB, EF // AK.

Ta có \(AB \bot AK\), \(AK \bot SD\), suy ra \(AK \bot SC\). Do EF // AK, suy ra ta cũng có \(EF \bot AB\) và EF cắt AB tại F, \(EF \bot SC\) và EF cắt SC tại E.

Các kết quả trên chứng tỏ EF là đoạn vuông góc chung của AB và SC.

Trong tam giác SAD vuông cân tại A ta có \(AK = \frac{{SD}}{2} = \frac{{a\sqrt 2 }}{2}\).

Vậy \(d(AB,SC) = EF = AK = \frac{{a\sqrt 2 }}{2}\).

Cách 2. Ta có mặt phẳng (SCD) chứa SC và song song với AB, suy ra:

\(d(AB,SC) = d(AB,(SCD)) = d(A,(SCD)) = AK = \frac{{a\sqrt 2 }}{2}\).