Cách tính khoảng cách từ điểm đến mặt phẳng - Toán 11

Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn MH được gọi là khoảng cách từ M đến (P), kí hiệu d(M, (P)).

Quy ước: \(d(M,(P)) = 0 \Leftrightarrow M \in (P)\).

Cách tính khoảng cách từ điểm M đến mặt phẳng (P):

B1: Xác định hình chiếu vuông góc H của M trên (P).

B2: Tính MH.

Ví dụ minh hoạ:

1) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, O là giao điểm của AC và BD, \(SO \bot (ABCD)\), SO = a. Tính:

a) Khoảng cách từ điểm S đến mặt phẳng (ABCD);

b) Khoảng cách từ điểm B đến mặt phẳng (SAC).

Giải:

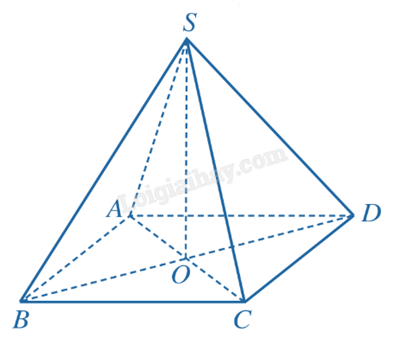
a) Ta có: \(O \in (ABCD)\), \(SO \bot (ABCD)\). Suy ra khoảng cách từ điểm S đến mặt phẳng (ABCD) là SO = a.

b) Do \(SO \bot (ABCD)\), \(BO \subset (ABCD)\) nên \(SO \bot BO\).

Vì BO vuông góc với hai đường thẳng AC và SO cắt nhau trong (SAC) nên \(BO \bot (SAC)\). Do \(O \in (SAC)\), \(BO \bot (SAC)\) nên khoảng cách từ B đến mặt phẳng (SAC) là \(BO = \frac{{a\sqrt 2 }}{2}\).

2) Cho hình chóp đều S.ABC. Biết độ dài cạnh đáy, cạnh bên tương ứng bằng a, b (\(a < b\sqrt 3 \)). Tính chiều cao của hình chóp.

Giải:

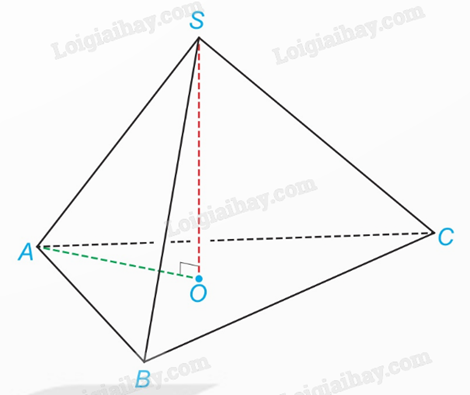
Hình chiếu của S trên mặt phẳng (ABC) là tâm O của tam giác đều ABC.

Trong tam giác đều ABC, ta có \(OA = \frac{a}{{\sqrt 3 }}\).

Trong tam giác vuông SOA, ta có \(SO = \sqrt {S{A^2} - O{A^2}}  = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \).

Vậy chiều cao của hình chóp là \(SO = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \).