Bài tập 34 trang 124 Tài liệu dạy – học Toán 7 tập 2

Giải bài tập Cho tam giác DEF cân tại D, kẻ trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho MN = ME.

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho tam giác DEF cân tại D, kẻ trung tuyến EM. Trên tia đối của tia ME lấy điểm N sao cho

MN = ME.

a) Chứng minh DE = FN và tam giác DFN cân.

b) Trên tia đối của FD, lấy điểm A sao cho FA = FD. Chứng minh F là trọng tâm của tam giác NEA.

c) Chứng minh tam giác DNA vuông

d) Kẻ đường cao EB của tam giác AEN. Chứng minh ba điểm E, F, B thẳng hàng.

Lời giải chi tiết

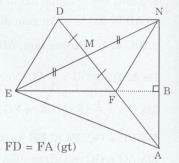
a) Xét ∆DEM và ∆FNM

Ta có: DM = MF (M là trung điểm của DF)

\(\widehat {DME} = \widehat {NMF}\) (đối đỉnh)

EM = MN (gt)

Do đó: ∆DEM = ∆FNM (c.g.c) => DE = FN

Mà DE = DF (∆DEF cân tại D). Nên FN=DF

Do đó ∆DNF cân tại F.

b) Ta có \(MF = {1 \over 2}FD\) (M là trung điểm của DF) và FD = FA (gt)

\( \Rightarrow MF = {1 \over 2}FA \Rightarrow {{MF} \over {FA}} = {1 \over 2} \Rightarrow {{AM - FA} \over {FA}} = {1 \over 2} \Rightarrow {{AM} \over {FA}} - 1 = {1 \over 2} \Rightarrow {{AM} \over {FA}} = {3 \over 2} \Rightarrow AF = {2 \over 3}AM\)

∆EAN có AM là đường trung tuyến (EM = MN, \(M \in EN\))

F thuộc đoạn thẳng AM và \(AF = {2 \over 3}AM\)

Do đó F là trọng tâm của tam giác NEA.

c) Ta có FN = FA (= DF) => ∆FAN cân tại F \( \Rightarrow \widehat {FNA} = \widehat {FAN}\)

Mà \(\widehat {FND} = \widehat {FDN}\) (∆DNF cân tại F). Do đó \(\widehat {DNA} = \widehat {FND} + \widehat {FNA} = \widehat {FAN} + \widehat {FDN}\)

∆DNA có \(\widehat {DNA} + \widehat {FAN} + \widehat {FDN} = 180^\circ\)

Do đó \(\widehat {DNA} + \widehat {DNA} = 180^\circ \Rightarrow 2\widehat {DNA} = 180^\circ \Rightarrow \widehat {DNA} = 90^\circ\)

Vậy tam giác DNA vuông tại N.

d) Xét ∆DMN và ∆EMF ta có: DM = MF

\(\widehat {NMD} = \widehat {EMF}\) (đối đỉnh)

MN = EM (gt)

Do đó: ∆DMN = ∆FME (c.g.c) \( \Rightarrow \widehat {DNM} = \widehat {MEF}\)

Mà \(\widehat {DNM}\) và \(\widehat {MEF}\) ở vị trí so le trong. Nên DN // EF

Mặt khác \(DN \bot NA\) (∆DNA vuông tại N). Do đó \(EF \bot NA\)

Ta có: \(EF \bot NA\) và \(EB \bot NA\) (EB là đường cao của ∆AEN)

Do đó EF trùng với EB. Vậy E, F, B thẳng hàng.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.2 trên 6 phiếu

Bài tiếp theo

Bài tập 35 trang 124 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A có góc A nhọn. Tia phân giác của góc BAC cắt BC tại M.
Bài tập 36 trang 125 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A. Trung tuyến BM và CN cắt nhau tại H.
Bài tập 37 trang 125 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC vuông cân tại A có AM là trung tuyến. Lấy điểm D bất kì thuộc cạnh BC. Gọi H và K theo thứ tự là hình chiếu vuông góc cuả B và C xuống đường thẳng AD.
Bài tập 38 trang 125 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A có AM là đường trung tuyến, D là điểm tùy ý thuộc AM. Chứng minh điểm D cách đều AB và AC.
Bài tập 39 trang 125 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Hai thị trấn A và B nằm gần hai trục đường cùng dẫn đến nhà máy C chuyên sản xuất sữa (hình 75). Để mở rộng thị trường tiêu thụ và thuận lợi cho việc phân phối sữa,
Bài tập 40 trang 125 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Tia AH cắt A, đường cao BE và CF cắt nhau tại H. Tia AH cắt BC tại I. Chứng minh I là trung điểm của BC.
Bài tập 33 trang 124 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC tại D. Kẻ DE vuông góc với BC
Bài tập 32 trang 124 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác MNP cân tại M (MN = MP > NP). Đường trung trực của MP tại D cắt đường thẳng NP tại E. Trên tia đối của tia DE lấy điểm F sao cho MF = EP.
Bài tập 31 trang 124 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC cân tại A, đường cao AD, G là trọng tâm. Trên tia đối của tia DG lấy điểm E sao cho DE = DG.
Bài tập 30 trang 124 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Cho tam giác ABC vuông tại A (AB < AC)
Bài tập 29 trang 124 Tài liệu dạy – học Toán 7 tập 2
Giải bài tập Một bác thợ mộc muốn cắt một mặt bàn hình tròn có kích thước lớn nhất từ một tấm gỗ hình tam giác (hình 74). Em hãy vẽ lại hình ảnh tấm gỗ hình tam giác trên giấy và đề xuất phương án giúp bác thợ mộc cắt được mặt bàn hình tròn theo yêu cầu.