Phương trình đường thẳng trong không gian - Toán 12

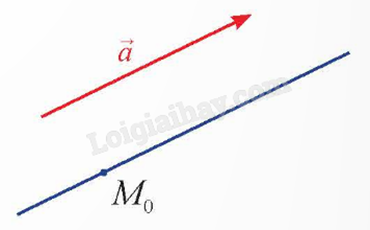
Vecto \(\overrightarrow a  \ne \overrightarrow 0 \) có giá song song hoặc trùng với đường thẳng d được gọi là vecto chỉ phương của d.

Trong không gian Oxyz, cho đường thẳng d đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow a  = ({a_1};{a_2};{a_3})\). Hệ phương trình

\(\left\{ \begin{array}{l}x = {x_0} + {a_1}t\\y = {y_0} + {a_2}t\\z = {z_0} + {a_3}t\end{array} \right.\)

được gọi là phương trình tham số của đường thẳng d (t là tham số, \(t \in R\)).

Ví dụ minh hoạ:

Trong không gian Oxyz, cho đường thẳng d đi qua điểm M(2;−2;1) và có vecto chỉ phương là \(\overrightarrow a  = (1; - 1;2)\). Viết phương trình tham số của đường thẳng d.

Giải:
Phương trình tham số của d là \(\left\{ \begin{array}{l}x = 2 + t\\y =  - 2 - t\\z = 1 + 2t\end{array} \right.\) \((t \in \mathbb{R})\).

Trong không gian Oxyz, cho đường thẳng d đi qua điểm \({M_0}({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow a  = ({a_1};{a_2};{a_3})\) với \({a_1}\), \({a_2}\), \({a_3}\) đều khác 0.

Hệ phương trình

\(\frac{{x - {x_0}}}{{{a_1}}} = \frac{{y - {y_0}}}{{{a_2}}} = \frac{{z - {z_0}}}{{{a_3}}}\)

được gọi là phương trình chính tắc của đường thẳng d.

Ví dụ minh hoạ:

Trong không gian Oxyz, viết phương trình chính tắc của đường thẳng d, biết d đi qua điểm M(4;2;−1) và có vecto chỉ phương \(\overrightarrow a  = ( - 1; - 4;3)\).

Giải:

Phương trình chính tắc của đường thẳng d là \(\frac{{x - 4}}{{ - 1}} = \frac{{y - 2}}{{ - 4}} = \frac{{z + 1}}{3}\).