Lý thuyết Tích phân Toán 12 Kết nối tri thức

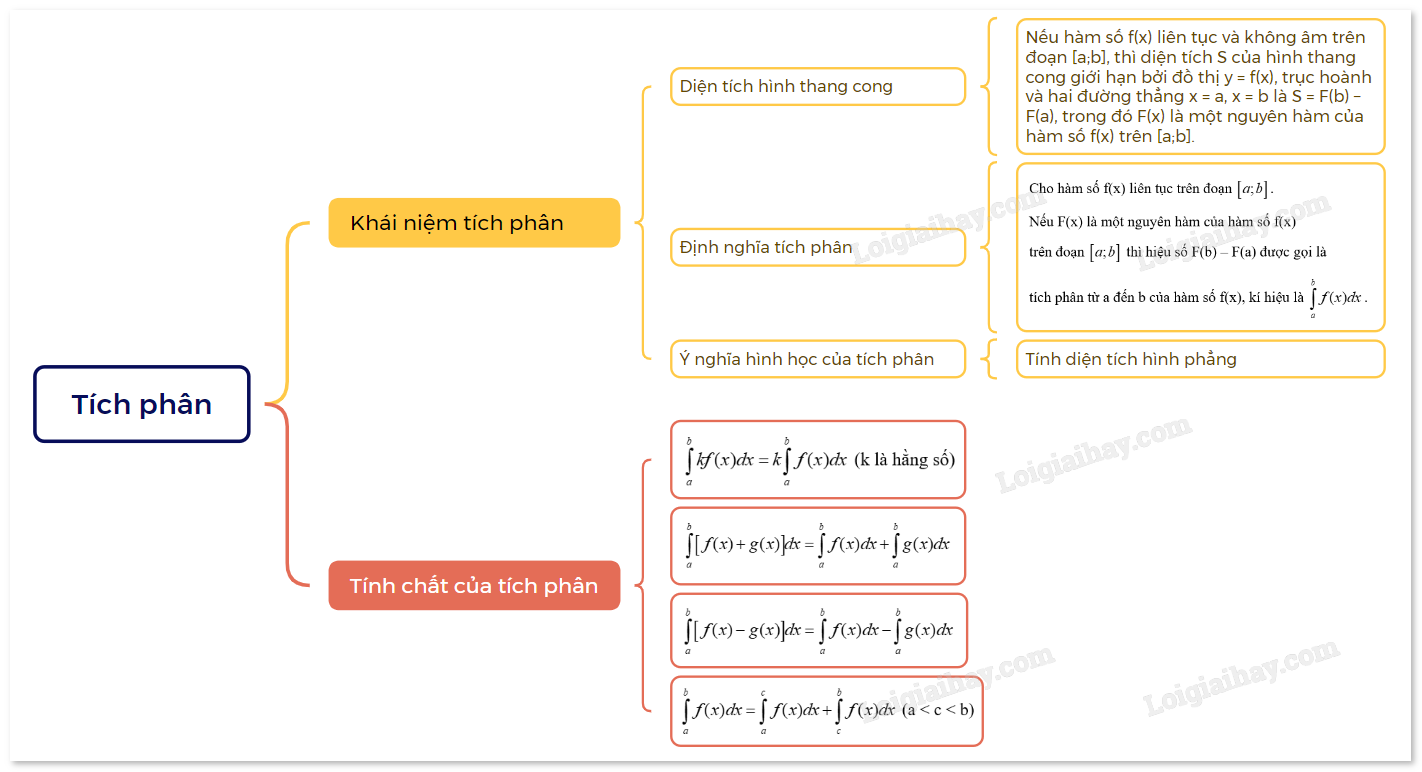
1.Khái niệm tích phân a) Diện tích hình thang cong

1.Khái niệm tích phân

a) Diện tích hình thang cong

Nếu hàm số f(x) liên tục và không âm trên đoạn \(\left[ {a;b} \right]\), thì diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b là S = F(b) – F(a), trong đó F(x) là một nguyên hàm của hàm số f(x) trên \(\left[ {a;b} \right]\).

b) Định nghĩa tích phân

Cho hàm số f(x) liên tục trên đoạn \(\left[ {a;b} \right]\). Nếu F(x) là một nguyên hàm của hàm số f(x) trên đoạn \(\left[ {a;b} \right]\) thì hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là \(\int\limits_a^b {f(x)dx} \).

Ý nghĩa hình học của tích phân:

Nếu hàm số f(x) liên tục và không âm trên đoạn \(\left[ {a;b} \right]\), thì tích phân \(\int\limits_a^b {f(x)dx} \) là diện tích S của hình thang cong giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = a, x = b.

2. Tính chất của tích phân

\(\int\limits_a^b {kf(x)dx = k\int\limits_a^b {f(x)dx} } \) (k là hằng số)
\(\int\limits_a^b {\left[ {f(x) + g(x)} \right]} dx = \int\limits_a^b {f(x)dx + \int\limits_a^b {g(x)dx} } \)
\(\int\limits_a^b {\left[ {f(x) - g(x)} \right]} dx = \int\limits_a^b {f(x)dx - \int\limits_a^b {g(x)dx} } \)
\(\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx + \int\limits_c^b {f(x)dx} } } \) (a<c<b)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 12,13,14 SGK Toán 12 tập 2 - Kết nối tri thức
Khái niệm tích phân
Giải mục 2 trang 16,17 SGK Toán 12 tập 2 - Kết nối tri thức
Tính chất của tích phân
Giải bài tập 4.8 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Sử dụng ý nghĩa hình học của tích phân, tính: a) \(\int\limits_1^2 {\left( {2x + 1} \right)dx} \); b) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} dx} \).
Giải bài tập 4.9 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Cho \(\int\limits_0^3 {f\left( x \right)dx = 5} \) và \(\int\limits_0^3 {g\left( x \right)dx = 2} \). Tính: a) \(\int\limits_0^3 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} \); b) \(\int\limits_0^3 {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} \); c) \(\int\limits_0^3 {3f\left( x \right)dx} \); d) \(\int\limits_0^3 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]dx} \).
Giải bài tập 4.10 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Tính: a) \(\int\limits_0^3 {{{\left( {3x - 1} \right)}^2}dx} \); b) \(\int\limits_0^{\frac{\pi }{2}} {\left( {1 + \sin x} \right)dx} \); c) \(\int\limits_0^1 {\left( {{e^{2x}} + 3{x^2}} \right)dx} \); d) \(\int\limits_{ - 1}^2 {\left| {2x + 1} \right|dx} \).
Giải bài tập 4.11 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Một vật chuyển động dọc theo một đường thẳng sao cho vận tốc của nó tại thời điểm t (giây) là \(v\left( t \right) = {t^2} - t - 6\) (m/s). a) Tìm độ dịch chuyển của vật trong khoảng thời gian \(1 \le t \le 4\), tức là tính \(\int\limits_1^4 {v\left( t \right)dt} \). b) Tìm tổng quãng đường vật đi được trong khoảng thời gian này, tức là tính \(\int\limits_1^4 {\left| {v\left( t \right)} \right|dt} \).
Giải bài tập 4.12 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Giả sử lợi nhuận biên (tính bằng triệu đồng) của một sản phẩm được mô hình hóa bằng công thức \(P'\left( x \right) = - 0,0005x + 12,2\). Ở đây P(x) là lợi nhuận (tính bằng triệu đồng) khi bán được x đơn vị sản phẩm. a) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 101 đơn vị sản phẩm. b) Tìm sự thay đổi của lợi nhuận khi doanh số tăng từ 100 lên 110 đơn vị sản phẩm.
Giải bài tập 4.13 trang 18 SGK Toán 12 tập 2 - Kết nối tri thức
Giả sử vận tốc v của dòng máu ở khoảng cách r từ tâm của động mạch bán kính R không đổi, có thể được mô hình hóa bởi công thức \(v = k\left( {{R^2} - {r^2}} \right)\), trong đó k là một hằng số. Tìm vận tốc trung bình (đối với r) của động mạch trong khoảng \(0 \le r \le R\). So sánh vận tốc trung bình với vận tốc lớn nhất.