-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Lý thuyết Phép quay Toán 9 Cùng khám phá
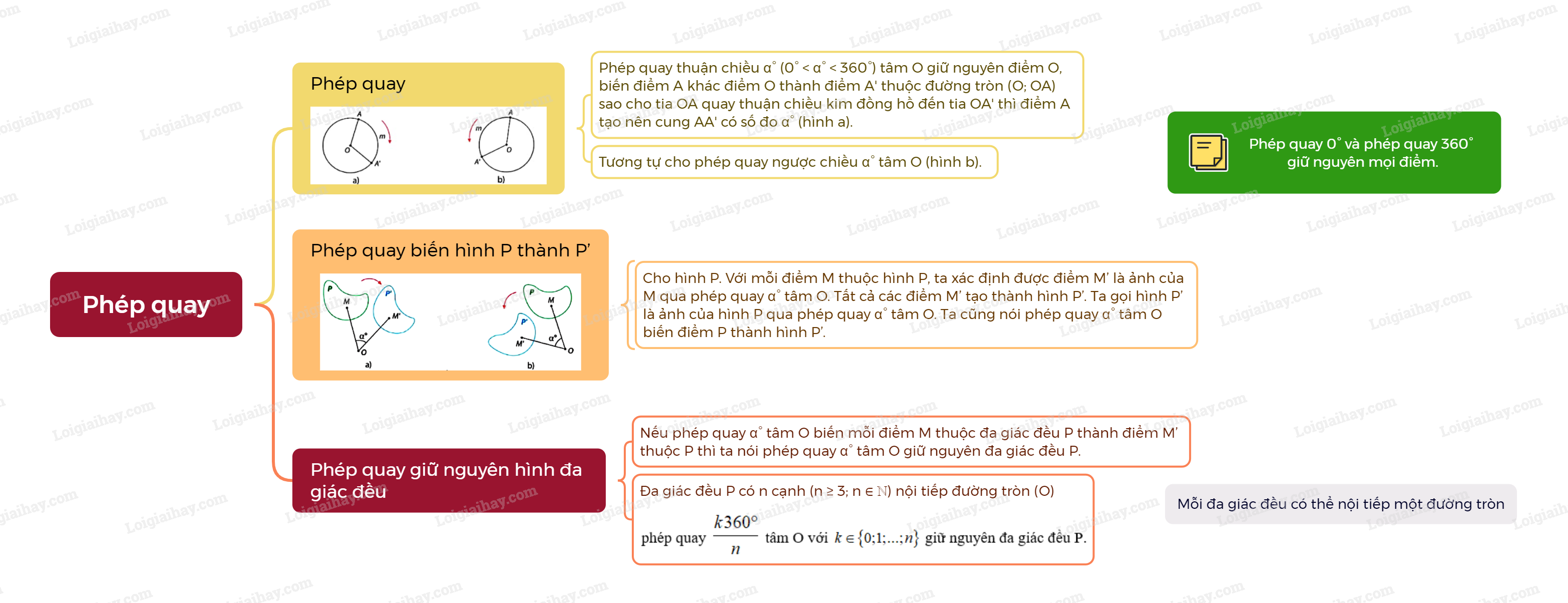
Khái niệm phép quay Phép quay thuận chiều (alpha ^circ ) (0° < (alpha ^circ ) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AmA’ có số đo (alpha ^circ ) (hình a).
Khái niệm phép quay
|
Phép quay thuận chiều \(\alpha ^\circ \) (0° < \(\alpha ^\circ \) < 360°) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm A’ thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AmA’ có số đo \(\alpha ^\circ \) (hình a). Định nghĩa tương tự cho phép quay ngược chiều \(\alpha ^\circ \) tâm O (hình b). Chú ý: Phép quay 0° và phép quay 360° giữ nguyên mọi điểm.
Nếu phép quay \(\alpha ^\circ \) tâm O biến điểm A thành điểm A’ thì điểm A’ được gọi là ảnh của điểm A qua phép quay này. |
Phép quay biến hình P thành P’
|
Cho hình P. Với mỗi điểm M thuộc hình P, ta xác định được điểm M’ là ảnh của M qua phép quay \(\alpha ^\circ \) tâm O. Tất cả các điểm M’ tạo thành hình P’. Ta gọi hình P’ là ảnh của hình P qua phép quay \(\alpha ^\circ \) tâm O. Ta cũng nói phép quay \(\alpha ^\circ \) tâm O biến điểm P thành hình P’.
|
Phép quay giữ nguyên đa giác đều
|
Nếu phép quay \(\alpha ^\circ \) tâm O biến mỗi điểm M thuộc đa giác đều P thành điểm M’ thuộc P thì ta nói phép quay \(\alpha ^\circ \) tâm O giữ nguyên đa giác đều P. |
Lưu ý: Người ta chứng minh được rằng mỗi đa giác đều có thể nội tiếp một đường tròn. Cho đa giác đều P có n cạnh (\(n \in \mathbb{R},n \ge 3\)) nội tiếp đường tròn (O), phép quay \(\frac{{k360^\circ }}{n}\) tâm O với \(k \in \left\{ {0;1;...;n} \right\}\) giữ nguyên đa giác đều P.
Ví dụ:
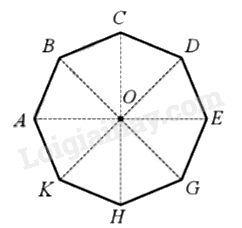
Ta có AB = BC = CD = DE = EG = GH = HK = KA nên số đo các cung nhỏ AB, BC, CD, DE, EG, GH, HK, KA đều bằng \(\frac{{360^\circ }}{8} = 45^\circ \).
Các phép quay thuận chiều (hoặc ngược chiều) \(45^\circ ,90^\circ ,135^\circ ,180^\circ ,225^\circ ,270^\circ ,315^\circ \) tâm O giữ nguyên bát giác ABCDEGHK.
Bình luận
Chia sẻ
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
