Bài 11. Phân tích một số ra thừa số nguyên tố

Lý thuyết Phân tích một số ra thừa số nguyên tố Toán 6 Cánh diều

Lý thuyết Phân tích một số ra thừa số nguyên tố Toán 6 Cánh diều ngắn gọn, đầy đủ, dễ hiểu

I. Cách tìm một ước nguyên tố của một số:

Để tìm một ước nguyên tố của số tự nhiên n lớn hơn 1, ta có thể làm như sau: Lần lượt làm phép chia n cho các số nguyên tố theo thứu tự tăng dần: 2;3;5;7;11;13;...

Khi đó, phép chia hết đầu tiên cho ta số chia là một ước nguyên tố của n

II.Phân tích một số ra thừa số nguyên tố

- Phân tích một số tự nhiên lớn hơn $1$ ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.

- Viết các thừa số nguyên tố theo thứ tự từ bé đến lớn, tích các thừa số giống nhau dưới dạng lũy thừa.

Sơ đồ cây:

Bước 1: Phân tích số n thành tích của hai số bất kì khác 1 và chính nó.

Bước 2: Tiếp tục phân tích ước thứ nhất và ước thứ hai thành tích của hai số bất kì khác 1 và chính nó.

Bước 3: Cứ như vậy đến khi nào xuất hiện số nguyên tố thì dừng lại.

Bước 4: Số n bằng tích của các số cuối cùng của mỗi nhánh.

Ví dụ:

Phân tích số 12 ra thừa số nguyên tố bằng sơ đồ cây:

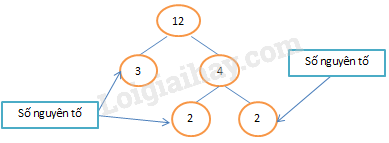
Như vậy $12 = {2^2}.3$

Sơ đồ cột:

Chia số $n$ cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng $1.$

Ví dụ: Số $76$ được phân tích như sau:

\[76\]	\[2\]
\[38\]	\[2\]
\[19\]	\[19\]
\[1\]

Như vậy $76 = {2^2}.19$

CÁC DẠNG TOÁN VỀ PHÂN TÍCH MỘT SỐ RA THỪA SỐ NGUYÊN TỐ

I. Phân tích các số cho trước ra thừa số nguyên tố

Phương pháp:

Ta thường phân tích một số tự nhiên $n\left( {n > 1} \right)$ ra thừa số nguyên tố bằng 2 cách:

+ Sơ đồ cây

+ Phân tích theo hàng dọc.

II. Ứng dụng phân tích một số ra thừa số nguyên tố để tìm các ước của số đó

Phương pháp:

+ Phân tích số cho trước ra thừa số nguyên tố.

+ Chú ý rằng nếu $c = a.b$ thì $a$ và $b$ là hai ước của $c.$

$a = b.q$$ \Leftrightarrow a \vdots b \Leftrightarrow a \in B\left( b \right)$ và $b \in $Ư$\left( a \right)$ $(a,b,q \in N,b \ne 0)$

III. Bài toán đưa về việc phân tích một số ra thừa số nguyên tố

Phương pháp:

Phân tích đề bài, đưa về việc tìm ước của một số cho trước bằng cách phân tích số đó ra thừa số nguyên tố.

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 8 phiếu

Bài tiếp theo

Trả lời Hoạt động 1 trang 44 SGK Toán 6 Cánh Diều
a) Hãy nêu các số nguyên tố nhỏ hơn 30. b) Tìm một ước nguyên tố của 91
Luyện tập vận dụng 1 trang 44 SGK Toán 6 Cánh Diều
Tìm một ước nguyên tố của 187.
Trả lời Hoạt động 2 trang 44 SGK Toán 6 Cánh Diều
Viết số 12 thành tích của các thừa số nguyên tố.
Trả lời Luyện tập vận dụng 2 trang 45 SGK Toán 6 Cánh Diều
Phân tích số 40 ra thừa số nguyên tố bằng cách viết “rẽ nhánh” và “theo cột dọc”.
Trả lời Luyện tập vận dụng 3 trang 45 SGK Toán 6 Cánh Diều
Phân tích số 450 ra thừa số nguyên tố.
Giải Bài 1 trang 46 SGK Toán 6 Cánh Diều Tập 1
Phân tích các số nguyên ra thừa số nguyên tố: 45, 78, 270, 299
Giải Bài 2 trang 46 SGK Toán 6 Cánh Diều Tập 1
a) Biết 400 = 2^4.5^2. Hãy viết 800 thành tích các thừa số nguyên tố b) Biết 320 = 2^6.5. Hãy viết 3200 thành tích các thừa số nguyên tố
Giải Bài 3 trang 46 SGK Toán 6 Cánh Diều Tập 1
a) Biết 2700 = 2^2.3^3.5^2. Hãy viết 270 và 900 thành tích các thừa số nguyên tố b) Biết 3600 = 2^4.3^2.5^2. Hãy viết 180 và 600 thành tích các thừa số nguyên tố
Giải Bài 4 trang 46 SGK Toán 6 Cánh Diều Tập 1
Hãy chỉ ra 2 số tự nhiên mà mỗi số đó có đúng 3 ước nguyên tố
Giải Bài 5 trang 46 SGK Toán 6 Cánh Diều Tập 1
Phân tích số 84 ra thừa số nguyên tố rồi tìm tập hợp các ước số của nó.