Toán 6, giải toán lớp 6 kết nối tri thức với cuộc sống Bài 19. Hình chữ nhật. Hình thoi. Hình bình hành. Hình ..

Lý thuyết Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân Toán 6 KNTT với cuộc sống


Lý thuyết Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân Toán 6 KNTT với cuộc sống ngắn gọn, đầy đủ, dễ hiểu

I. Hình chữ nhật

1. Nhận biết hình chữ nhật

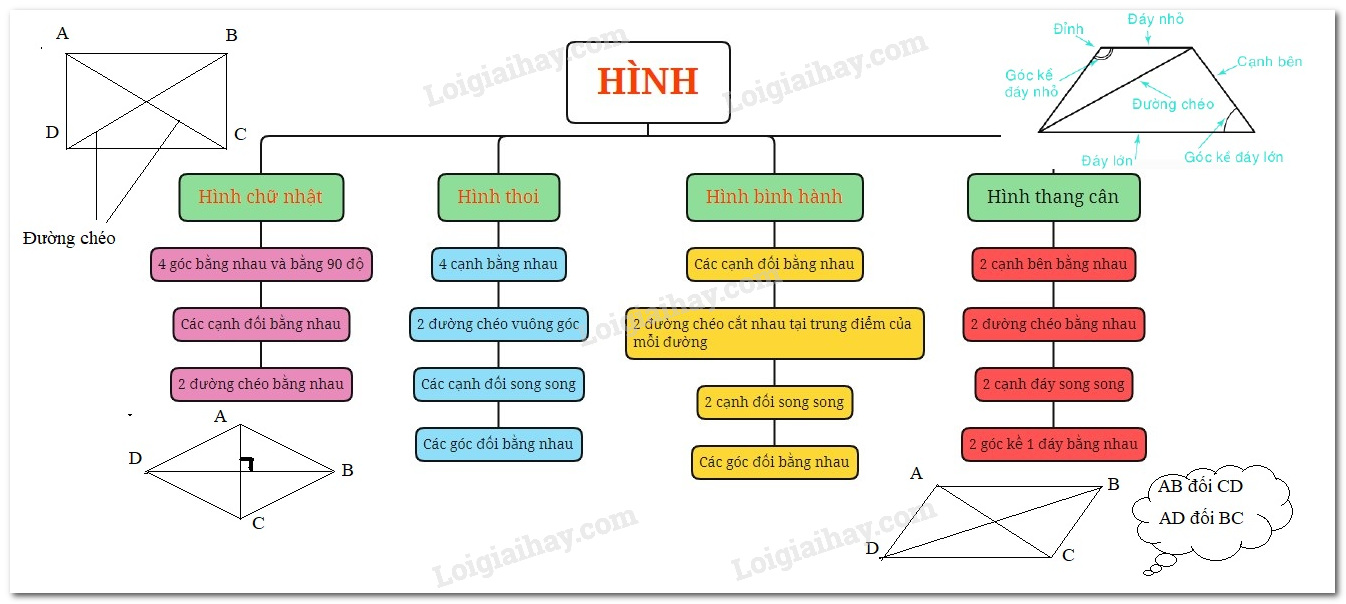
Một số yếu tố cơ bản của hình chữ nhật

 

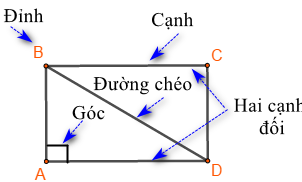
- Bốn góc bằng nhau và bằng \({90^0}\)

- Các cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

2.Cách vẽ hình chữ nhật

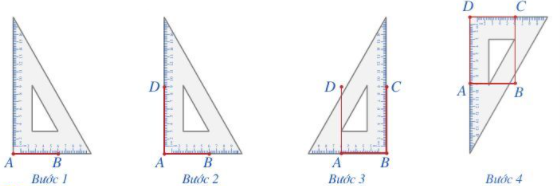
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB có độ dài bằng 6 cm

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD có độ dài bằng 9 cm

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC có độ dài bằng 9 cm

Bước 4. Vẽ đoạn thẳng CD.

II. Hình thoi

1. Một số yếu tố cơ bản của hình thoi

 

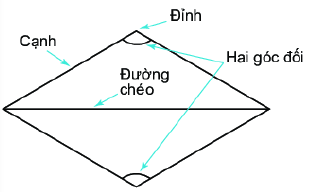
- Bốn cạnh bằng nhau

- Hai đường chéo vuông góc với nhau.

- Các cạnh đối song song với nhau

- Các góc đối bằng nhau

2. Vẽ hình thoi

Ví dụ: Dùng thước và compa vẽ hình thoi \(ABCD\), biết \(AB = 5\,cm\) và \(AC = 8\,cm\).

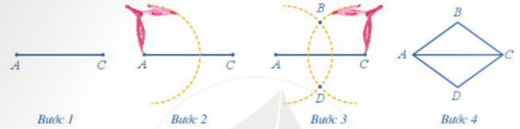
Bước 1. Dùng thước vẽ đoạn thẳng \(AC = 8\,cm\)

Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính \(5\,cm\).

Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính \(5\,cm\); phần đường tròn này cắt phần đường tròn tấm A vẽ ở Bước 2 tại các điểm B và D.

Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.

III. Hình bình hành

1.Nhận biết hình bình hành

Hình bình hành ABCD có:

- Bốn đỉnh A, B, C, D.

- Hai cặp cạnh đối diện bằng nhau: \(AB = CD;\,BC = AD\).

- Hai cặp cạnh đối diện song song: \(AB\) song song với \(CD\); \(BC\) song song với \(AD\).

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường: \(OA = OC;\,OB = OD.\)

- Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.

2.Cách vẽ hình bình hành

Ví dụ: Cho trước hai đoạn thẳng AB,AD như hình dưới đây. Vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.

Cách vẽ:

Ta có thể vẽ bằng thước và compa như sau:

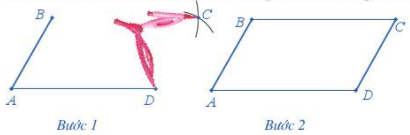
Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này

Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.

IV. Hình thang cân

1. Nhận biết hình thang cân

 

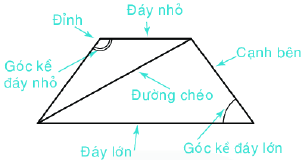
Hình thang cân có: 

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau

- Hai đáy song song với nhau

- Hai góc kề một đáy bằng nhau.

Ví dụ:

 

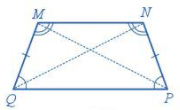
Hình thang cân \(MNPQ\) có:

- Hai cạnh cạnh đáy song song: \(MN\) song song với \(PQ\).

- Hai cạnh bên bằng nhau: \(MQ = NP\).

- Hai đường chéo bằng nhau: \(MP = NQ\).

- Hai góc kề với cạnh cạnh bên \(PQ\) bằng nhau, tức là hai góc \(NPQ\) và \(PQM\) bằng nhau; hai góc kề với cạnh bên \(MN\) bằng nhau, tức là hai góc \(QMN\) và \(MNP\) bằng nhau.

2.Cách gấp hình thang cân

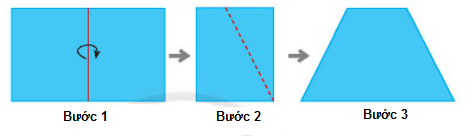
Bước 1: Gấp đôi một tờ giấy hình chữ nhật

Bước 2: Vẽ một đoạn thẳng nối hai điểm tùy ý trên hai cạnh đối diện (Cạnh không chứa nếp gấp). Cắt theo đường nét đứt như hình minh họa.

Bước 3: Mở tờ giấy ra ta được một hình thang cân.


Bình chọn:
4.6 trên 13 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 6 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store