Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống

Bài 22. Hai đường thẳng vuông góc Toán 11 Kết nối tri t..

Lý thuyết Hai đường thẳng vuông góc - Toán 11 Kết nối tri thức

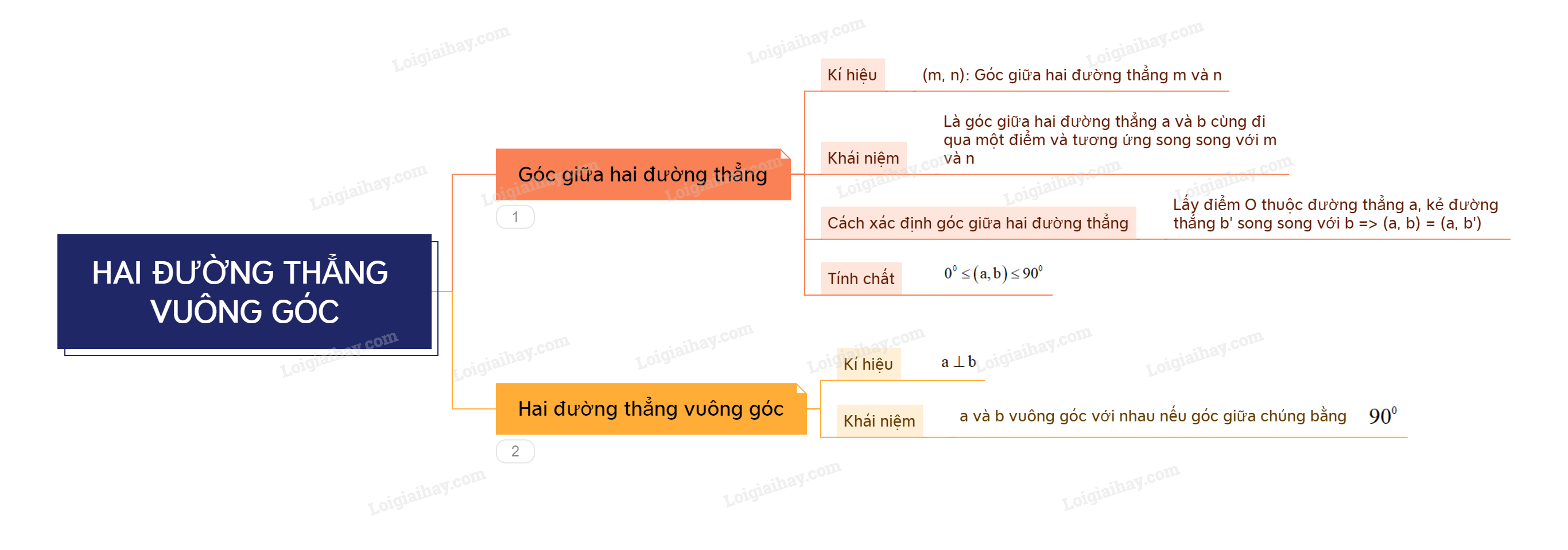
1. Góc giữa hai đường thẳng

1. Góc giữa hai đường thẳng

Góc giữa hai đường thẳng m và n trong không gian, kí hiệu (m, n), là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.

Chú ý:

- Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b’ song song với b. Khi đó \(\left( {a,b} \right) = \left( {a,b'} \right)\).

- Với hai đường thẳng a, b bất kì: \({0^0} \le \left( {a,b} \right) \le {90^0}\).

2. Hai đường thẳng vuông góc

Hai đường thẳng a, b được gọi là vuông góc với nhau, kí hiệu \(a \bot b\), nếu góc giữa chúng bằng \({90^0}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 28, 29 SGK Toán 11 tập 2 - Kết nối tri thức
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O'
Giải mục 2 trang 29, 30 SGK Toán 11 tập 2 - Kết nối tri thức
Đối với hai cánh cửa trong Hình 7.5, tính góc giữa hai đường mép cửa BC và MN
Bài 7.1 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
Cho hình lăng trụ ABC.A'B'C' có các đáy là các tam giác đều
Bài 7.2 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
Cho hình hộp ABCD.A'B'C'D' có các cạnh bằng nhau.
Bài 7.3 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
Cho tứ diện ABCD có (widehat {CBD} = {90^0}.)
Bài 7.4 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
Đối với nhà gỗ truyền thống, trong các cấu kiện hoành, quá giang, xà cái, rui, cột tương ứng được đánh số 1, 2, 3, 4, 5

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục

TẢI APP ĐỂ XEM OFFLINE

Bài giải mới nhất