Toán 6, giải toán lớp 6 kết nối tri thức với cuộc sống Bài 2. Cách ghi số tự nhiên - Toán 6 Kết nối tri thức v..

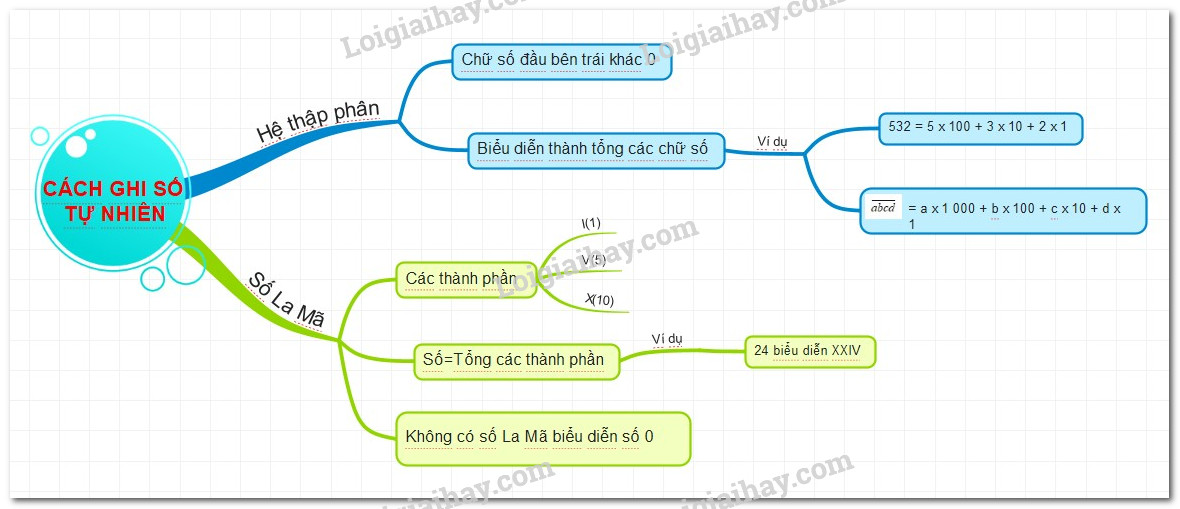
Lý thuyết Cách ghi số tự nhiên Toán 6 Kết nối tri thức với cuộc sống

Tải về

Lý thuyết Cách ghi số tự nhiên Toán 6 Kết nối tri thức với cuộc sống ngắn gọn, đầy đủ, dễ hiểu

Biểu diễn 1 số dưới dạng tổng các chữ số của nó

I. Hệ thập phân

1. Cách ghi số tự nhiên trong hệ thập phân

Để ghi số tự nhiên trong hệ thập phân, người ta dùng mười chữ số là \(0;1;2;3;4;5;6;7;8;9.\) Người ta lấy các chữ số trong 10 chữ số này rồi viết liền nhau thành một dãy, vị trí của các chữ số đó trong dãy gọi là hàng.

Trong hệ thập phân, cứ 10 đơn vị của một hàng thì làm thành 1 đơn vị của hàng liền trước đó. Ví dụ 10 chục thì bằng 1 trăm; mười trăm thì bằng 1 nghìn;...

Chú ý: Khi viết các số tự nhiên, ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên bên trái khác 0.

2. Đối với các số có 4 chữ số khác 0 trở lên, ta viết tách riêng từng lớp. Mỗi lớp là một nhóm 3 chữ só từ phải sang trái.

3. Với những số tự nhiên có nhiều chữ số, mỗi chữ số ở các vị trí (hàng) khác nhau thì có giá trị khác nhau

Ví dụ:

Số 120 250 160 555

- Đọc: Một trăm hai mươi tỉ, hai trăm năm mươi triệu một trăm sáu mươi nghìn năm trăm năm mươi lăm.

- Các lớp: lớp tỉ, triệu, nghìn, đơn vị được ghi lại như sau:

Lớp

Tỉ

Triệu

Nghìn

Đơn vị

Hàng

Trăm tỉ

Chục tỉ

Tỉ

Trăm triệu

Chục triệu

Triệu

Trăm nghìn

Chục nghìn

Nghìn

Trăm

Chục

Đơn vị

Chữ số

1

2

0

2

5

0

1

6

0

5

5

5

- Cùng là số 2 nhưng số 2 ở hàng chục tỉ có giá trị khác với số 2 ở hàng trăm triệu.

2. Cấu tạo thập phân của một số

+ Kí hiệu \(\overline {ab} \) chỉ số tự nhiên có hai chữ số, chữ số hàng chục là \(a\left( {a \ne 0} \right)\), chứ số hàng đơn vị là \(b\). Ta có:

\(\overline {ab}  = \left( {a \times 10} \right) + b\) với \(a \ne 0.\)

+ Kí hiệu \(\overline {abc} \) chỉ số tự nhiên có 3 chữ số, chữ số hàng trăm là \(a\left( {a \ne 0} \right)\),  chữ số hàng chục là \(b\), chữ số hàng đơn vị là \(c\). Ta có:

\(\overline {abc}  = a.100 + b.10 + c\) với \(a \ne 0.\)

+ Với các số tự nhiên cụ thể thì không có dấu gạch ngang trên đầu.

Ví dụ:

\(\begin{array}{l}\overline {2b}  = 2.10 + b\\\overline {a5b}  = a.100 + 5.10 + b\left( {a \ne 0} \right)\end{array}\)

\(\overline {a03bcd}  = a.100000 + 0.10000\)\( + 3.1000 + b.100 + c.10 + d\)\(\left( {a \ne 0} \right)\)

II. Hệ La Mã

Cách viết số La Mã: Ta chỉ viết các số La Mã không quá 30.
+ Các thành phần để ghi số La Mã:
- Các kí tự  I, V, X : Các chữ số La Mã.
- Các cụm chữ số IV, IX
- Giá trị của các thành phần này không thay đổi dù ở vị trí nào.

Thành phần

I

V

X

IV

IX

Giá trị (viết trong hệ thập phân)

1

5

10

4

9
 
Các số La Mã biểu diễn các số từ 1 đến 10

I

II

III

IV

V

VI

VII

VIII

IX

X

1

2

3

4

5

6

7

8

9

10
 
Các số La Mã biểu diễn các số từ 11 đến 20: Thêm X vào bên trái mỗi số từ I đến X

XI

XII

XIII

XIV

XV

XVI

XVII

XVIII

XIX

XX

11

12

13

14

15

16

17

18

19

20
 
Các số La Mã biểu diễn các số từ 21 đến 30: Thêm XX vào bên trái mỗi số từ I đến X

XXI

XXII

XXIII

XXIV

XXV

XXVI

XXVII

XXVIII

XXIX

XXX

21

22

23

24

25

26

27

28

29

30
 
Chú ý:
- Mỗi số La Mã biểu diễn một số tự nhiên bằng tổng giá trị của các thành phần tạo nên số đó.
- Không có số La Mã nào biểu diễn số 0.
Ví dụ:
Số XIII có 4 thành phần là X, I, I, I tương ứng với các giá trị 10,1,1,1. Do đó biểu diễn số 10+1+1+1=13.
Viết số 17 thành số La Mã:
Số 7 được viết là VII
Số 17 = 7+10, tức là số 7 thêm 10 đơn vị nên ta thêm chữ X trước VII được: XVII

Bình chọn:
4.4 trên 30 phiếu
Tải về
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 6 - Kết nối tri thức - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store