Toán 11, giải toán lớp 11 cánh diều

Bài 2. Đường thẳng vuông góc với mặt phẳng Toán 11 Cánh..

Giải mục 3 trang 81, 82 SGK Toán 11 tập 2 - Cánh Diều

Cho điểm O và đường thẳng a.

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Cánh diều

Toán - Văn - Anh - Lí - Hóa - Sinh

Lựa chọn câu để xem lời giải nhanh hơn

Hoạt động 3

Cho điểm O và đường thẳng a. Gọi b, c là hai đường thẳng phân biệt cùng đi qua điểm O và cùng vuông góc với đường thẳng a (Hình 14).

a) Mặt phẳng (P) đi qua hai đường thẳng b, c có vuông góc với đường thẳng a hay không?

b) Có bao nhiêu mặt phẳng đi qua điểm O và vuông góc với đường thẳng a?

Phương pháp giải:

Quan sát hình vẽ để trả lời

Lời giải chi tiết:

a) Ta có

\(\left\{ \begin{array}{l}a \bot b \subset \left( P \right)\\a \bot c \subset \left( P \right)\\b\cap c\end{array} \right. \Rightarrow a \bot \left( P \right)\)

b) Chỉ có 1 mặt phẳng duy nhất đi qua điểm O và vuông góc với a

Luyện tập - vận dụng 2

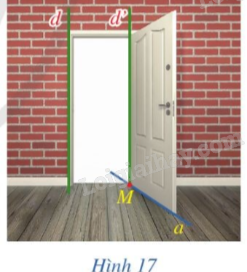
Hình 17 mô tả một cửa gỗ có dạng hình chữ nhật, ở đó nẹp cửa và mép dưới cửa lần lượt gợi nên hình ảnh hai đường thẳng d và a. Điểm M là vị trí giao giữa mép gắn bản lề và mép dưới của cửa. Hãy giải thích tại sao khi quay cánh cửa, mép dưới cửa là những đường thẳng a luôn nằm trên mặt phẳng đi qua điểm M cố định và vuông góc với đường thẳng d.

Phương pháp giải:

Quan sát hình vẽ để trả lời

Lời giải chi tiết:

Vì sàn nhà là một mặt phẳng vuông góc với đường thẳng d. Mà đường thẳng a luôn nằm trên mặt phẳng đó nên đường thẳng d luôn vuông góc với đường thẳng a

Hoạt động 4

Cho mặt phẳng (P) và điểm O. Gọi a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P) sao cho a và b không đi qua O. Lấy hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b (Hình 18).

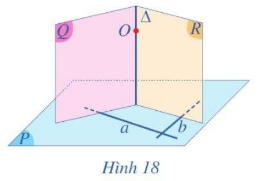
a) Giao tuyến ∆ của hai mặt phẳng (Q), (R) có vuông góc với mặt phẳng (P) hay không?

b) Có bao nhiêu đường thẳng đi qua O và vuông góc với (P)?

Phương pháp giải:

Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.

Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với 2 đường thẳng cắt nhàu nằm trong mặt phẳng đó.

Lời giải chi tiết:

a) Ta có:

\(\left\{ \begin{array}{l}a \bot \left( Q \right)\\\Delta \subset \left( Q \right)\end{array} \right. \Rightarrow a \bot \Delta \)

\(\left\{ \begin{array}{l}b \bot \left( R \right)\\\Delta \subset \left( R \right)\end{array} \right. \Rightarrow b \bot \Delta \)

Vì \(\left\{ \begin{array}{l}\Delta \bot a \subset \left( R \right)\\\Delta \bot b \subset \left( R \right)\\a\cap b\end{array} \right. \Rightarrow \Delta \bot \left( R \right)\)

b) Chỉ có duy nhất 1 đường thẳng đi qua O và vuông góc với (P)

Luyện tập - vận dụng 3

Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, \(a \bot (P)\). Giả sử điểm M thỏa mãn \(OM \bot (P)\). Chứng minh rằng \(M \in a\).

Phương pháp giải:

Chỉ có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.

Lời giải chi tiết:

Vì chỉ có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước nên nếu \(\left\{ \begin{array}{l}a \cap (P) = O\\a \bot (P)\\OM \bot (P)\end{array} \right. \Rightarrow M \in a\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 4 trang 83, 84 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 19, hai thanh sắt và bản phẳng để ngồi gợi nên hình ảnh hai đường thẳng a, b và mặt phẳng (P).
Giải mục 5 trang 85 SGK Toán 11 tập 2 - Cánh Diều
Trong mặt phẳng (P). Xét một điểm M tùy ý trong không gian.
Giải mục 6 trang 87 SGK Toán 11 tập 2 - Cánh Diều
Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P)
Bài 1 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Quan sát Hình 30 (hai cột của biển báo, mặt đường)
Bài 2 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC).
Bài 3 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho tứ diện ABCD có (AB bot (BCD)), các tam giác BCD và ACD là những tam giác nhọn.
Bài 4 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho tứ diện ABCD có (AB bot (BCD),BC bot CD). Gọi M và N lần lượt là hình chiếu vuông góc của B trên AC và AD. Chứng minh rằng:
Bài 5 trang 88 SGK Toán 11 tập 2 – Cánh Diều
Cho hình chóp O.ABC có (widehat {AOB} = widehat {BOC} = widehat {COA} = 90^circ ). Chứng minh rằng:
Giải mục 2 trang 81 SGK Toán 11 tập 2 - Cánh Diều
Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d
Giải mục 1 trang 80 SGK Toán 11 tập 2 - Cánh Diều
Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà.
Giải hoạt động mở đầu trang 80 SGK Toán 11 tập 2 – Cánh Diều
Trong Hình 9, cột gỗ thẳng đứng và sàn nhà nằm ngang gợi nên hình ảnh đường thẳng vuông góc với mặt phẳng.
Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Cánh diều
1. Định nghĩa Đường thẳng d được gọi là vuông góc với mặt phẳng (P) nếu đường thẳng d vuông góc với mọi đường thẳng a nằm trong mặt phẳng (P), kí hiệu \(d \bot \left( P \right)\) hoặc \(\left( P \right) \bot d\).