Bài 2. Tam giác bằng nhau trang 48 SGK Toán 7 chân trời..

Giải mục 3 trang 55, 56, 57 SGK Toán 7 tập 2 - Chân trời sáng tạo

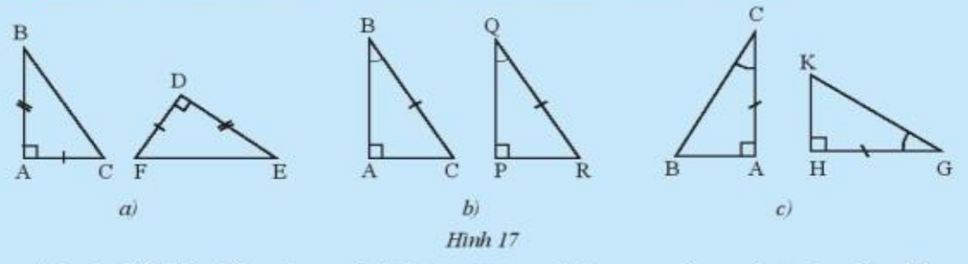
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.

Video hướng dẫn giải

Lựa chọn câu để xem lời giải nhanh hơn

HĐ 5

Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.

Phương pháp giải:

Dựa vào tam giác vuông có sẵn 1 cặp góc bằng nhau ( góc vuông ) nên chỉ cần tìm điều kiện để các cặp cạnh, cặp góc còn lại bằng nhau

Lời giải chi tiết:

a) Xét \(\Delta{ABC}\) và \(\Delta{DEF}\) có:

AB = DE (gt)

\(\widehat {BAC} = \widehat {EDF}\) (gt)

AC = DF (gt)

\(\Rightarrow \Delta{ABC}=\Delta{DEF}\) ( c-g-c )

b) Ta có: \(\widehat B + \widehat C = \widehat Q + \widehat R = 90^0\)

Mà \(\widehat B = \widehat Q\) \( \Rightarrow \widehat C = \widehat R\)

Xét \(\Delta{ABC}\) và \(\Delta{PQR}\) có:

\(\widehat C = \widehat R\) (gt)

BC = QR (gt)

\(\widehat B = \widehat Q\) (gt)

\(\Rightarrow \Delta{ABC}=\Delta{PQR}\) ( g-c-g )

c) Xét \(\Delta{ABC}\) và \(\Delta{HKG}\) có:

\(\widehat C = \widehat G\) (gt)

AC = HG (gt)

\(\widehat A = \widehat H\) (gt)

\(\Rightarrow \Delta{ABC}=\Delta{HKG}\) ( g-c-g )

TH 4

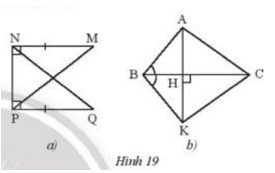
Tìm các tam giác vuông bằng nhau trong mỗi hình bên (Hình 19).

Phương pháp giải:

Sử dụng các trường hợp bằng nhau của tam giác vuông

Lời giải chi tiết:

a) Xét \(\Delta{MNP} và \Delta{QPN}\), ta có:

NM = PQ

NP chung

\(\widehat {MNP} = \widehat {NPQ}\)

\(\Rightarrow \Delta{MNP} =\Delta{QPN}\) (c.g.c)

b) Ta thấy\(\Delta{ABH}=\Delta{KBH}\) (g-c-g) và \(\Delta{AHC}=\Delta{KHC}\)(c-g-c)

\(\Delta{ABC}=\Delta{KBC}\)

HĐ 6

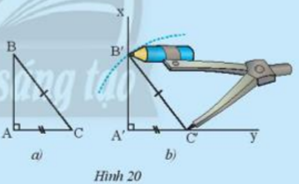
Cho tam giác ABC vuông tại A trong Hình 20a. Vẽ lên tờ giấy tam giác vuông A’B’C’có cạnh huyền và một cạnh góc vuông bằng với cạnh huyền và một cạnh góc vuông của tam giác ABC như sau:

- Vẽ góc vuông xA’ý, trên cạnh A’y vẽ đoạn A’C’= AC.

- Vẽ cung tròn tâm C’ bán kính bằng BC cắt A’x tại B’

Cắt rời tam giác A’B’C’. Em hãy cho biết có thể đặt chồng khít tam giác này lên tam giác kia không.

Phương pháp giải:

- Ta vẽ 2 cạnh trước rồi sau đó vẽ góc

- Cắt và so sánh 2 hình

Lời giải chi tiết:

Ta nhận thấy 2 hình bằng nhau (chồng lên nhau vì vừa khít)

TH 5

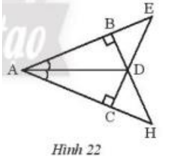
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.

Phương pháp giải:

- Sử dụng các trường hợp bằng nhau của tam giác: c-c-c; c-g-c; g-c-g

- Sử dụng các trường hợp bằng nhau của tam giác vuông: 2 cạnh góc vuông; cạnh góc vuông - góc nhọn kề; cạnh huyền - góc nhọn.

Lời giải chi tiết:

+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:

AD chung

\(\widehat {BAD} = \widehat {DAC}\) (gt)

\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)

\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)

\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)

+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:

BD = CD (cmt)

\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )

\( \Rightarrow \Delta{BED}=\Delta{CHD}\) (cạnh góc vuông - góc nhọn kề )

+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)

\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)

Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)

\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)

Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:

\(\widehat {BAD} = \widehat {DAC}\) (gt)

AD chung

\(\widehat {ADE} = \widehat {ADH}\) (cmt)

\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )

+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:

AB = AC (cmt)

\(\widehat {BAH}\) chung

\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 6 phiếu

Bài tiếp theo

Giải bài 1 trang 57 SGK Toán 7 tập 2 - Chân trời sáng tạo
Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.
Giải bài 2 trang 57 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho
Giải bài 3 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó
Giải bài 4 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho biết
Giải bài 5 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.
Giải bài 6 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
Giải bài 7 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của
Giải bài 8 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a)AD = BC
Giải bài 9 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.
Giải mục 2 trang 49, 50, 51, 52, 53, 54 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước: -Vẽ đoạn thẳng B’C’= BC -Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA. -Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung) -Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b) Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt
Giải mục 1 trang 48, 49 SGK Toán 7 tập 2 - Chân trời sáng tạo
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’