Giải bài 5 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo

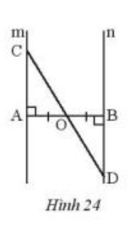
Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.

Tổng hợp đề thi giữa kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN...

Đề bài

Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm CD.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

- Chứng minh tam giác OAC và tam giác OBD bằng nhau

- Từ đó suy ra OC = OD ( 2 cạnh tương ứng)

Lời giải chi tiết

Xét \(\Delta OAC\) và \(\Delta OBD\), ta có:

\(\widehat {COA} = \widehat {BOD}\) ( 2 góc đối đỉnh)

AO = BO

\(\widehat A = \widehat B\)

\(\Rightarrow \Delta OAC=\Delta OBD\) ( g-c-g )

\( \Rightarrow CO = DO\) ( cạnh tương ứng )

\( \Rightarrow \) O là trung điểm CD

Bình luận

Chia sẻ

Bình chọn:

4.7 trên 29 phiếu

Bài tiếp theo

Giải bài 6 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
Giải bài 7 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của
Giải bài 8 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng: a)AD = BC
Giải bài 9 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.
Giải bài 4 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho biết
Giải bài 3 trang 58 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó
Giải bài 2 trang 57 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho
Giải bài 1 trang 57 SGK Toán 7 tập 2 - Chân trời sáng tạo
Quan sát Hình 23 rồi thay dấu ? bằng tên tam giác thích hợp.
Giải mục 3 trang 55, 56, 57 SGK Toán 7 tập 2 - Chân trời sáng tạo
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.
Giải mục 2 trang 49, 50, 51, 52, 53, 54 SGK Toán 7 tập 2 - Chân trời sáng tạo
Cho tam giác ABC như trong Hình 6a. Lấy một tờ giấy, trên đó vẽ tam giác A’B’C’có ba cạnh bằng ba cạnh của tam giác ABC (A’B’= AB, A’C’= AC, B’C’= BC) theo các bước: -Vẽ đoạn thẳng B’C’= BC -Vẽ cung tròn tâm B’có bán kính bằng BA, vẽ cung trong tâm C’ có bán kính bằng CA. -Hai cung tròn trên cắt nhau tại A’ (chỉ lấy một trong hai giao điểm của hai cung) -Vẽ các đoạn thẳng B’A, C’A’, ta được tam giác A’B’C’ (Hình 6b) Em hãy cắt rời tam giác A’B’C’ ra khỏi tờ giấy vừa vẽ và thử xem có thể đặt
Giải mục 1 trang 48, 49 SGK Toán 7 tập 2 - Chân trời sáng tạo
Dùng kéo cắt một tờ giấy thành hình tam giác ABC. Đặt tam giác lên tờ giấy thứ hai. Vẽ và cắt theo các cạnh của tam giác ABC thành tam giác A’B’C’ (Hình1). Hãy so sánh các cạnh và các góc của hai tam giác ABC và A’B’C’