Giải mục 2 trang 18, 19, 20 SGK Toán 10 tập 1 - Chân trời sáng tạo
Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích. Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không? Viết tất cả các tập con của tập hợp A = { a;b} .
HĐ Khám phá
Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.
a) \(A = \{ - 1;1\} \) và \(B = \{ - 1;0;1;2\} \)
b) \(A = \mathbb{N}\) và \(B = \mathbb{Z}\)
c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.
d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.
Lời giải chi tiết:
a) Có vì \( - 1 \in B,\;1 \in B\).
b) Có vì các số tự nhiên cũng là số nguyên.
c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.
d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.
Thực hành 4
Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?
a) \(A = \{ - \sqrt 3 ;\sqrt 3 \} \) và \(B = \{ x \in \mathbb{R}|{x^2} - 3 = 0\} \)
b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;
c) \(E = \{ x \in \mathbb{N}|x\) là ước của 12\(\} \) và \(F = \{ x \in \mathbb{N}|x\) là ước của 24\(\} .\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Phương pháp giải:
\(A \subset B\) nếu mọi phần tử của A đều là phần tử của B.
\(A = B\) nếu \(A \subset B\) và \(B \subset A\)
Lời giải chi tiết:
a) A là tập con củ B vì:
\( - \sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3 \in B\)
\(\sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3 \in B\)
Lại có: \({x^2} - 3 = 0 \Leftrightarrow x = \pm \sqrt 3 \) nên \(B = \{ - \sqrt 3 ;\sqrt 3 \} \).
Vậy A = B.
b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.
\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.
c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.
\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)
Thực hành 5
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Lời giải chi tiết:
Các tập con của tập hợp A là:
+) Tập con có 0 phần tử: \(\emptyset \) (tập hợp rỗng)
+) Tập hợp con có 1 phần tử: {a}, {b}
+) Tập hợp con có 2 phần tử: \(A = \{ a;b\} .\)
Chú ý
+) Mọi tập hợp A đều có 2 tập con là: \(\emptyset \) và A.
Vận dụng
Bạn An khẳng định rằng: Với các tập hợp A, B, C bất kì, nếu \(A \subset B\) và \(B \subset C\) thì \(A \subset C.\)
Khẳng định của bạn An có đúng không? Hãy giải thích bằng cách sử dụng biểu đồ Ven.
Lời giải chi tiết:
+) Biểu diễn: \(A \subset B\)
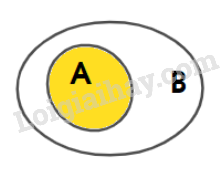
+) Sau đó, biểu diễn: \(B \subset C\)
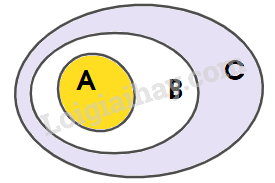
Quan sát biểu đồ Ven, dễ thấy \(A \subset C.\)
- Giải mục 3 trang 20 SGK Toán 10 tập 1 - Chân trời sáng tạo
- Giải bài 1 trang 20 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 2 trang 21 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 3 trang 21 SGK Toán 10 tập 1 – Chân trời sáng tạo
- Giải bài 4 trang 21 SGK Toán 10 tập 1 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ - SGK Toán 10 CTST
- Lý thuyết Xác suất của biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Không gian mẫu và biến cố - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Ba đường conic trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo
- Lý thuyết Đường tròn trong mặt phẳng tọa độ - SGK Toán 10 Chân trời sáng tạo












