Giải mục 2 trang 11, 12, 13 Chuyên đề học tập Toán 12 - Chân trời sáng tạo

Hoạt động 3

Trả lời câu hỏi Hoạt động 3 trang 11 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Xét tình huống thương nhân thu mua trái cây ở Bài toán mở đầu (trang 6).

a) Nếu gọi \(x,y\) (tính theo tấn) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua thì \(x\) và \(y\) phải thoả mãn hệ bất phương trình bậc nhất hai ẩn nào?

b) Từ đó, phát biểu bài toán quy hoạch tuyến tính tìm khối lượng thu mua mỗi loại trái cây để thu được lợi nhuận cao nhất. Giải bài toán đó.

Phương pháp giải:

‒ Biểu diễn các đại lượng chưa biết thông qua các đại lượng đã biết và ẩn để lập bài toán quy hoạch tuyến tính.

‒ Giải bài toán quy hoạch tuyến tính:

Bước 1: Biểu diễn tập phương án của bài toán trên mặt phẳng toạ độ \(Oxy\).

Bước 2: Tính giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\).

Trong trường hợp tập phương án là miền đa giác thì giá trị lớn nhất (nhỏ nhất) trong các giá trị này là giá trị lớn nhất (nhỏ nhất) của \(F\) trên \({\Omega }\).

Trong trường hợp tập phương án không là miền đa giác nằm trong góc phần tư thứ nhất và các hệ số \(a\) và \(b\) không âm thì giá trị nhỏ nhất trong các giá trị này là giá trị nhỏ nhất của \(F\) trên \({\Omega }\).

Lời giải chi tiết:

a) Gọi \(x,y\) tấn \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là khối lượng trái cây loại A và B được thương nhân thu mua.

Thương nhân đó mua tối đa 8 tấn trái cây nên ta có phương trình sau: \(x + y \le 8\).

Số tiền mua loại trái cây A là \(12{\rm{x}}\) triệu đồng.

Số tiền mua loại trái cây B là \(20{\rm{y}}\) triệu đồng.

Tổng số tiền mua trái cây không vượt quá 120 triệu đồng nên ta có phương trình sau: \(12{\rm{x}} + 20y \le 120\) hay \(3{\rm{x}} + 5y \le 30\).

Do đó ta có hệ bất phương trình sau: \(\left\{ \begin{array}{l}x + y \le 8\\3x + 5y \le 30\\x \ge 0\\y \ge 0\end{array} \right.\).

Lợi nhuận khi bán trái cây loại A là \(1,1{\rm{x}}\) triệu đồng.

Lợi nhuận khi bán trái cây loại B là \(1,5y\) triệu đồng.

Lợi nhuận thương nhân đó thu được là: \(F = 1,1{\rm{x}} + 1,5y\) triệu đồng.

b) Ta cần giải bài toán quy hoạch tuyến tính: \(F = 1,1x + 1,5y \to \max \), với ràng buộc \(\left\{ \begin{array}{l}x + y \le 8\\3x + 5y \le 30\\x \ge 0\\y \ge 0\end{array} \right.\)

Tập phương án \({\Omega }\) là miền tứ giác \(ABCD\).

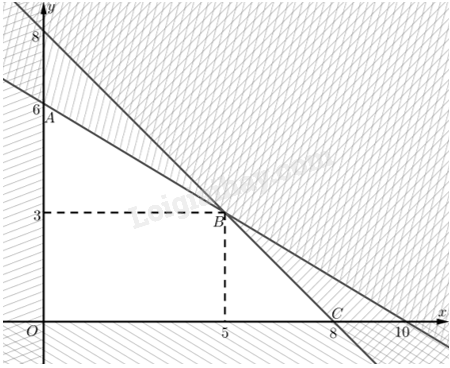
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}3{\rm{x}} + 5y = 30\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 6\end{array} \right.\). Vậy \(A\left( {0;6} \right)\).

Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}3{\rm{x}} + 5y = 30\\x + y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 3\end{array} \right.\). Vậy \(B\left( {5;3} \right)\).

Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y = 8\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 8\\y = 0\end{array} \right.\). Vậy \(C\left( {8;0} \right)\)

Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):

\(\begin{array}{l}F\left( {0;0} \right) = 1,1\,.0 + 1,5\,.0 = 0;F\left( {0;6} \right) = 1,1\,.0 + 1,5\,.6 = 9;\\F\left( {5;3} \right) = 1,1\,.5 + 1,5\,.3 = 10;F\left( {8;0} \right) = 1,1\,.8 + 1,5\,.0 = 8,8\end{array}\)

Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {5;3} \right) = 10\).

Vậy thương nhân cần mua 5 tấn loại A và 3 tấn loại B thì thu được lợi nhuận cao nhất.

Luyện tập 3

Trả lời câu hỏi Luyện tập 3 trang 13 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Một dây chuyền của nhà máy sản xuất đá xây dựng dự định sản xuất hai loại sản phẩm A và B. Thời gian để dây chuyền sản xuất 100 tấn sản phẩm loại A và 100 tấn sản phẩm loại B lần lượt là 2 giờ và 3 giờ. Do nhu cầu thị trường, xí nghiệp sản xuất sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm loại B. Sản phẩm loại A cho lợi nhuận là 5 triệu đồng/100 tấn; sản phẩm loại B cho lợi nhuận 9 triệu đồng/100 tấn.

Trong thời gian không quá 6 giờ làm việc của dây chuyền, cần sản xuất bao nhiêu tấn sản phẩm loại A, bao nhiêu tấn sản phẩm loại B để thu được lợi nhuận cao nhất?

Phương pháp giải:

Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.

Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.

Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.

Lời giải chi tiết:

Gọi \(x,y\) tấn \(\left( {x \ge 0,y \ge 0} \right)\) lần lượt là sản lượng sản phẩm loại A và loại B xí nghiệp đó sản xuất.

Do thời gian làm việc của dây chuyền không quá 6 giờ nên \(2x + 3y \le 6\) hay \(2x + 3y - 6 \le 0\).

Do sản lượng sản phẩm loại A không ít hơn 3 lần sản lượng sản phẩm B nên \(x \ge 3y\) hay \(x - 3y \ge 0\).

Lợi nhuận thu được là \(F = 5x + 9y\) (triệu đồng).

Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 5x + 9y \to \max \) với ràng buộc \(\left\{ \begin{array}{l}2x + 3y - 6 \le 0\\x - 3y \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)

Tập phương án \({\Omega }\) là miền tam giác \(OAB\).

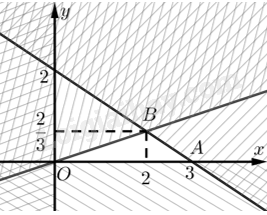
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 6\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 0\end{array} \right.\). Vậy \(A\left( {3;0} \right)\).

Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}2{\rm{x}} + 3y = 6\\x - 3y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = \frac{2}{3}\end{array} \right.\). Vậy \(B\left( {2;\frac{2}{3}} \right)\).

Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):

\(F\left( {0;0} \right) = 5.0 + 9.0 = 0;F\left( {3;0} \right) = 5.3 + 9.0 = 15;F\left( {2;\frac{2}{3}} \right) = 5.2 + 9.\frac{2}{3} = 16\)

Do đó: \(\mathop {\max }\limits_{\Omega } F = F\left( {2;\frac{2}{3}} \right) = 16\).

Vậy xí nghiệp cần sản xuất 200 tấn loại A và \(\frac{{200}}{3}\) tấn loại B thì thu được lợi nhuận cao nhất.

Luyện tập 4

Trả lời câu hỏi Luyện tập 4 trang 13 Chuyên đề học tập Toán 12 Chân trời sáng tạo

Trong 100 g thịt bò loại I có chứa 21 g protein và 3,5 g lipid; 100 g thịt bò loại II có chứa 18 g protein và 10,5 g lipid. Biết rằng thịt bò loại I có giá 220 nghìn đồng/kg thì thịt bò loại II có giá 210 nghìn đồng/kg. Để có lượng thực phẩm từ hai loại thịt bò trên cung cấp ít nhất 630 g protein và 210 g lipid, cần mua khối lượng bao nhiêu cho mỗi loại thịt bò loại I và II sao cho chi phí thấp nhất?

Phương pháp giải:

Bước 1: Đặt hai ẩn biểu thị hai đại lượng chưa biết (cần tìm). Viết điều kiện có nghĩa cho các ẩn đó.

Bước 2: Từ dữ kiện của bài toán, viết biểu thức biểu thị đại lượng cần tìm giá trị tối ưu và các bất phương trình bậc nhất đối với hai ẩn trên. Từ đó phát biểu bài toán quy hoạch tuyến tính nhận được.

Bước 3: Giải bài toán quy hoạch tuyến tính và trả lời.

Lời giải chi tiết:

Gọi \(x,y\) (\(x \ge 0,y \ge 0\), tính theo 100g) lần lượt là khối lượng của thịt bò loại I và loại II cần dùng.

Do cần cung cấp ít nhất 630g protein nên ta có \(21x + 18y \ge 630\) hay \(7x + 6y - 210 \ge 0\).

Do cần cung cấp ít nhất 210g lipid nên ta có \(3,5x + 10,5y \ge 210\) hay \(x + 3y - 60 \ge 0\).

Ta có: 220 nghìn đồng/kg=22 nghìn đồng/100g; 210 nghìn đồng/kg=21 nghìn đồng/100g.

Chi phí để mua thịt bò là \(F = 22x + 21y\) (nghìn đồng).

Từ đó, ta cần giải bài toán quy hoạch tuyến tính: \(F = 22x + 21y \to \min \) với ràng buộc \(\left\{ \begin{array}{l}7{\rm{x}} + 6y - 210 \ge 0\\x + 3y - 60 \ge 0\\x \ge 0\\y \ge 0\end{array} \right.\)

Tập phương án \({\Omega }\) của bài toán là miền không gạch (không là miền đa giác).

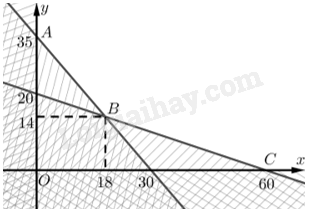
Toạ độ \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}7{\rm{x}} + 6y = 210\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 35\end{array} \right.\). Vậy \(A\left( {0;35} \right)\).

Toạ độ \(B\) là nghiệm của hệ \(\left\{ \begin{array}{l}7{\rm{x}} + 6y = 210\\x + 3y = 60\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 18\\y = 14\end{array} \right.\). Vậy \(B\left( {18;14} \right)\).

Toạ độ \(C\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + 3y = 60\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 60\\y = 0\end{array} \right.\). Vậy \(C\left( {60;0} \right)\).

Giá trị của biểu thức \(F\) tại các đỉnh của \({\Omega }\):

\(F\left( {0;35} \right) = 22.0 + 21.35 = 735;F\left( {18;14} \right) = 22.18 + 21.14 = 690;F\left( {60;0} \right) = 22.60 + 21.0 = 1320\)

Do đó: \(\mathop {\min }\limits_{\Omega } F = F\left( {18;14} \right) = 690\).

Vậy cần mua \(18.100g = 1,8kg\) thịt bò loại I và \(14.100g = 1,4kg\) thịt bò loại II.