Giải mục 1 trang 55, 56 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ1

Trả lời câu hỏi Hoạt động 1 trang 55 SGK Toán 10 Kết nối tri thức

Cho vecto \(\overrightarrow {AB}  = \overrightarrow a \). Hãy xác định điểm C sao cho \(\overrightarrow {BC}  = \overrightarrow a \).

a) Tìm mối quan hệ giữa \(\overrightarrow {AC} \) và \(\overrightarrow a  + \overrightarrow a \).

b) Vecto \(\overrightarrow a  + \overrightarrow a \) có mối quan hệ như thế nào về hướng và độ dài đối với vecto \(\overrightarrow a \).

Phương pháp giải:

Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.

Lời giải chi tiết:

Xác định điểm C:

Trên tia AB lấy điểm C sao cho BC = a và B nằm giữa A, C.

a) Vì \(\overrightarrow {AB}  = \overrightarrow a  = \overrightarrow {BC} \) nên A, B, C thẳng hàng và B là trung điểm của AC.

Vậy \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow {AC} \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AC} } \right|\).

b) Ta có:  \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow {AB} } \right|\).

Mà \(\overrightarrow {AB}  = \overrightarrow a \) nên:  \(\overrightarrow a  + \overrightarrow a \) và \(\overrightarrow a \) cùng hướng, \(\left| {\overrightarrow a  + \overrightarrow a } \right| = 2.\left| {\overrightarrow a } \right|\).

CH1

Trả lời câu hỏi Câu hỏi trang 55 SGK Toán 10 Kết nối tri thức

\(1\overrightarrow a \) và \(\overrightarrow a \) có bằng nhau hay không?

Phương pháp giải:

Hai vecto bằng nhau nếu chúng có cùng độ dài và cùng hướng.

Lời giải chi tiết:

Ta có: Vecto \(1\overrightarrow a \) cùng hướng với vecto \(\overrightarrow a \) và \(\left| {1\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).

Vậy hai vecto \(1\overrightarrow a \) và \(\overrightarrow a \) bằng nhau.

HĐ2

Trả lời câu hỏi Hoạt động 2 trang 56 SGK Toán 10 Kết nối tri thức

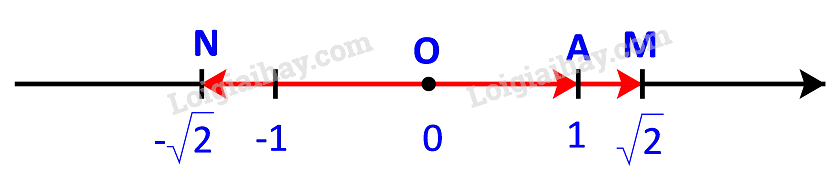
Trên một trục số, gọi O, A, M, N tương ứng biểu diễn các số \(0;\;1;\;\sqrt 2 ;\; - \sqrt 2 \). Hãy nêu mối quan hệ về hướng và độ dài của mỗi vecto \(\overrightarrow {OM} ,\;\overrightarrow {ON} \) với vecto \(\overrightarrow a  = \overrightarrow {OA} \). Viết đẳng thức thể hiện mối quan hệ giữa hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \).

Phương pháp giải:

Vecto \(k\;\overrightarrow a \) (với \(k > 0,\;\overrightarrow a  \ne \overrightarrow 0 \)) là vecto cùng hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(k\;\left| {\overrightarrow a } \right|\).

Lời giải chi tiết:

Dễ thấy:

Vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) có cùng giá nên chúng cùng phương.

Mà vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) cùng nằm trên tia OM nên chúng cùng chiều.

Vậy vecto \(\overrightarrow {OM} \) và \(\overrightarrow {OA} \) cùng hướng.

Ngoài ra, \(\left| {\overrightarrow {OM} } \right| = OM = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\)

\( \Rightarrow \left| {\overrightarrow {OM} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\)

Ta kết luận \(\overrightarrow {OM}  = \sqrt 2 .\overrightarrow {OA} \).

Dễ thấy:

Vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) có cùng giá nên chúng cùng phương.

Mà vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) thuộc hai tia đối nhau nên chúng ngược chiều.

Vậy vecto \(\overrightarrow {ON} \) và \(\overrightarrow {OA} \) ngược hướng.

Ngoài ra, \(\left| {\overrightarrow {ON} } \right| = ON = \sqrt 2 \) và \(\left| {\overrightarrow {OA} } \right| = OA = 1\).

\( \Rightarrow \left| {\overrightarrow {ON} } \right| = \sqrt 2 .\left| {\overrightarrow {OA} } \right|\).

Ta kết luận \(\overrightarrow {ON}  = -\sqrt 2 .\overrightarrow {OA} \).

CH2

Trả lời câu hỏi Câu hỏi trang 56 SGK Toán 10 Kết nối tri thức

\( - \;\overrightarrow a \) và \( - 1\;\overrightarrow a \) có mối quan hệ gì?

Phương pháp giải:

Vecto \(k\;\overrightarrow a \) (với \(k < 0,\;\overrightarrow a  \ne \overrightarrow 0 \))  là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| k \right|\;\left| {\overrightarrow a } \right|\).

Lời giải chi tiết:

Ta có:

Vecto \( - \overrightarrow a \) là vecto đối của vecto \(\overrightarrow a \).

\( \Rightarrow  - \overrightarrow a \) ngược hướng với vecto \(\overrightarrow a \) và \(\left| { - \overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).

Lại có:

Vecto  \( - 1\overrightarrow a \) là vecto ngược hướng với vecto \(\overrightarrow a \) và có độ đài bằng \(\left| { - 1} \right|\left| {\overrightarrow a } \right| = \left| {\overrightarrow a } \right|\).

\( \Rightarrow  - \overrightarrow a \) và \( - 1\overrightarrow a \) cùng hướng và có độ dài bằng nhau (bằng vecto\(\overrightarrow a \)).

Hay \( - \overrightarrow a  =  - 1\overrightarrow a \).

LT1

Trả lời câu hỏi Luyện tập 1 trang 56 SGK Toán 10 Kết nối tri thức

Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?

a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để \(\overrightarrow {AM}  = t.\overrightarrow {AB} \).

b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM}  = \frac{{AM}}{{AB}}.\overrightarrow {AB} \).

c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số \(t \le 0\) để \(\overrightarrow {AM}  = t.\overrightarrow {AB} \).

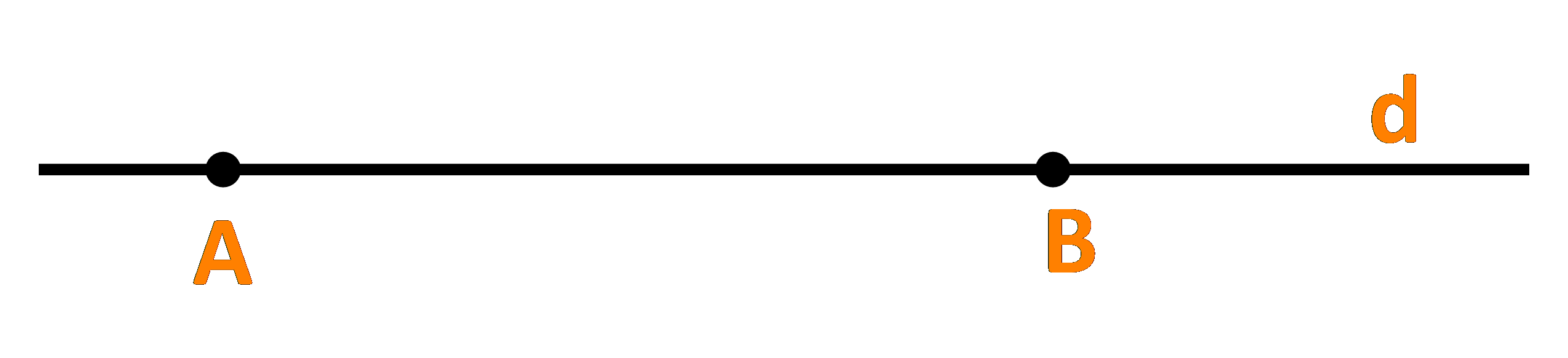
Phương pháp giải:

\(\overrightarrow a \) và \(\overrightarrow b \;\left( {\overrightarrow b  \ne \overrightarrow 0 } \right)\) cùng phương khi và chỉ khi tồn tại số k để \(\overrightarrow a  = k.\overrightarrow b \).

Nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng thì \(k = \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\).

Nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng thì \(k =  - \frac{{|\overrightarrow a |}}{{|\overrightarrow b |}}\).

Lời giải chi tiết:

a) Điểm M thuộc đường thẳng d khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng phương (cùng giá d).

Khi và chỉ khi tồn tại số t để \(\overrightarrow {AM}  = t.\overrightarrow {AB} \).

Vậy khẳng định a) đúng.

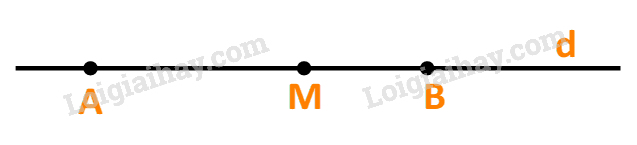
b) Với điểm M bất kì, ta luôn có \(\overrightarrow {AM}  = \frac{{AM}}{{AB}}.\overrightarrow {AB} \).

Sai vì \(\overrightarrow {AM}  = \frac{{AM}}{{AB}}.\overrightarrow {AB} \) khi và chỉ khi \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) cùng hướng.

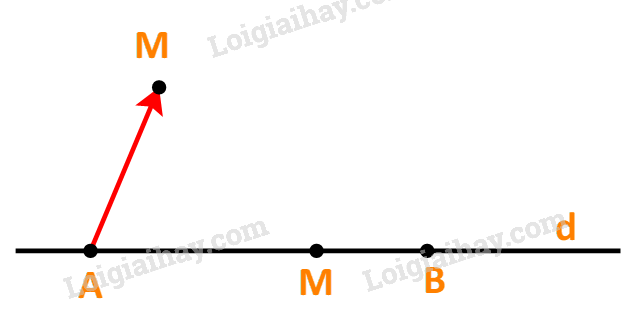
c) Điểm M thuộc tia đối của tia AB, tức là A nằm giữa M và B.

Khi và chỉ khi hai vecto \(\overrightarrow {AM} \) và \(\overrightarrow {AB} \) ngược hướng khi và chỉ khi tồn tại số \(t < 0\) để \(\overrightarrow {AM}  = t.\overrightarrow {AB} \).

Vậy khẳng định c) sai.