Toán 8, giải toán lớp 8 chân trời sáng tạo Bài 2. Các phép toán với đa thức nhiều biến Toán 8 chân..

Giải mục 1 trang 12 SGK Toán 8 tập 1– Chân trời sáng tạo


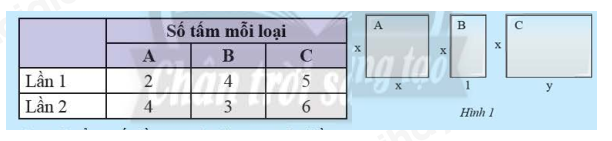
Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng , và với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá đồng/ . Tại đây có hai lần nhập vật liệu như bảng sau:

Lựa chọn câu để xem lời giải nhanh hơn

HĐ1

Video hướng dẫn giải

Tại một công trình xây dựng, người ta dùng ba loại tấm kính chống nắng \(A\), \(B\) và \(C\) với các kích thước như Hình 1 (tính bằng m). Giá tiền các tấm kính được tính theo diện tích với đơn giá \(a\) đồng/\({m^2}\). Tại đây có hai lần nhập vật liệu như bảng sau:

 

a) Tính tổng số tiền mua kính của cả hai lần.

b) Số tiền lần 2 nhiều hơn lần 1 bao nhiêu?

Phương pháp giải:

Sử dụng công thức tính diện tích hình vuông, hình chữ nhật để tính được số tiền mua kính.

Lời giải chi tiết:

a) Diện tích tấm kính chống nắng \(A\) là: \(x.x = {x^2}\) (\({m^2}\))

Diện tích tấm kính chống nắng \(B\) là: \(x.1 = x\) (\({m^2}\))

Diện tích tấm kính chống nắng \(C\) là: \(x.y = xy\) (\({m^2}\))

Số tiền mua kính lần 1 là: \(\left( {2{x^2} + 4x + 5xy} \right).a\) (đồng)

Số tiền mua kính lần 2 là: \(\left( {4{x^2} + 3x + 6xy} \right).a\) (đồng)

Tổng số tiền mua kính cả hai lần là: \(\left( {2{x^2} + 4x + 5xy} \right).a + \left( {4{x^2} + 3x + 6xy} \right).a = \left( {2{x^2} + 4x + 5xy + 4{x^2} + 3x + 6xy} \right).a = \left( {6{x^2} + 7x + 11xy} \right).a\)

b) Số tiền lần 2 nhiều hơn lần 1 là:

\(\left( {4{x^2} + 3x + 6xy} \right).a - \left( {2{x^2} + 4x + 5xy} \right).a = \left( {4{x^2} + 3x + 6xy - 2{x^2} - 4x - 5xy} \right).a = \left( {2{x^2} - x + xy} \right).a\)

Thực hành 1

Video hướng dẫn giải

Cho hai đa thức \(M = 1 + 3xy - 2{x^2}{y^2}\) và \(N = x - xy + 2{x^2}{y^2}\). Tính \(M + N\) và \(M - N\).

Phương pháp giải:

Muốn cộng hay trừ hai đa thức ta làm như sau:

- Viết hai đa thức trong ngoặc và nối với nhau bằng dấu cộng hay trừ.

- Bỏ dấu ngoặc rồi thu gọn đa thức thu được.

Lời giải chi tiết:

Ta có:

\(M + N = \left( {1 + 3xy - 2{x^2}{y^2}} \right) + \left( {x - xy + 2{x^2}{y^2}} \right)\)

\(M + N = 1 + 3xy - 2{x^2}{y^2} + x - xy + 2{x^2}{y^2}\)

\(M + N = \left( { - 2{x^2}{y^2} + 2{x^2}{y^2}} \right) + \left( {3xy - xy} \right) + x + 1\)

\(M + N = 2xy + x + 1\)

Ta có:

\(M - N = \left( {1 + 3xy - 2{x^2}{y^2}} \right) - \left( {x - xy + 2{x^2}{y^2}} \right)\)

\(M - N = 1 + 3xy - 2{x^2}{y^2} - x + xy - 2{x^2}{y^2}\)

\(M - N = \left( { - 2{x^2}{y^2} - 2{x^2}{y^2}} \right) + \left( {3xy + xy} \right) - x + 1\)

\(M - N =  - 4{x^2}{y^2} + 4xy - x + 1\)


Bình chọn:
4.3 trên 9 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Chân trời sáng tạo - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store